Abstract
The increasing demand of efficient optoelectronic devices such as photovoltaics has created a great research interest in methods to manipulate the electronic and optical properties of all the layers of the device. Tin dioxide (SnO2), due to his charge transport capability, high stability and easy fabrication is the main electron transport layer in modern photovoltaics which have achieved a record efficiency. While the wide band gap of SnO2 makes it an effective electron transport layer, its potential for other energy applications such as photocatalysis is limited. To further improve is conductivity and reduce its bandgap, doping or co-doping with various elements has been proposed. In the present density functional theory (DFT) study, we focus on the investigation of vanadium (V) and tantalum (Ta) doped SnO2 both in the bulk and the surface. Here we focus on interstitial and substitutional doping aiming to leverage these modifications to enhance the density of states for energy application. These changes also have the potential to influence the optical properties of the material, such as absorption, and make SnO2 more versatile for photovoltaic and photocatalytic applications. The calculations show the formation of gap states near the band edges which are beneficial for the electron transition and in the case of Ta doping the lowest bandgap value is achieved. Interestingly, in the case of Ta interstitial, deep trap states are formed which depending of the application could be advantageous. Regarding the optical properties, we found that V doping significantly increases the refractive index of SnO2 while the absorption is generally improved in all the cases. Lastly, we investigate the electronic properties of the (110) surface of SnO2, and we discuss possible other applications due to surface doping. The present work highlights the importance of V and Ta doping for energy applications and sensor applications.
Introduction
SnO2 also known as cassiterite and stannic oxide, represents one of the most used wide bandgap semiconductors in energy devices1,2. It is characterized by n-type conductivity, which can be attributed to its intrinsic defects, such as oxygen vacancies3 and tin interstitials4. As a compound, SnO2 exhibits low resistivity5 and high-dielectric constant, and has therefore been considered for gate oxides on Si-based electronic devices6,7 as well as for electron transport layer in perovskite photovoltaics8. Undoped SnO2 has a wide bandgap value of ~ 3.6 eV9 and its reported resistivity values range from 10−2 to 10−3 Ω cm10. One of the main quests in photovoltaic technologies is to enhance the conductivity of the electron transport layer without reducing the bandgap11. In essence, the efficiency of the devices is highly connected with the charge recombination and losses due to the limited transport properties of the used layers. Furthermore, the stoichiometric SnO2 exhibits low intrinsic carrier density and low mobility of its charges due to the oxygen vacancies which act as donors. Doping is examined as a strategy to further reduce the resistance of SnO2 and to enhance the transition in the visible wavelengths12,13. For photocatalysis, it is important to increase the conductivity of the photocatalyst and decrease the bandgap of the semiconductor. The increase in the carrier concentration makes the intermediate energy gap between valence band and conduction band more active14.
To further improve the response of gas sensing devices and improve the sensitivity and selectivity, it is common to add porous materials and catalytically active agents15,16. Doping the metal oxide -such as SnO2 – based sensor promotes the physicochemical reactions between the surface and the gas17. Various reports propose that incorporation of the appropriate dopant is an efficient technique to enhance the sensitivity, selectivity, operating temperature and recovery time of SnO2 based gas sensor as the dopant modifies the structural, electronic and optical properties of the host compound18,19. Transition metal elements such as Zn, Mn, Cr etc. have been proposed by researchers as successful dopants which enhance the response and selectivity of SnO220,21,22,23. Although various studies24,25,26 have explored the electrical and optical properties of Ta doped SnO2, the applications of this doping method in gas sensor has not be reported or examined. Interestingly, Liu et al.27 developed a Ta:SnO2 electron transport layer (ETL) for high efficiency perovskite solar cells. Ben Soltan et al.28 developed V:SnO2 nanoparticles for photocatalytic applications.
Here we employ hybrid functional DFT to investigate the impact of substitutional and interstitial doped V and Ta doped bulk and (110) surface SnO2.
Methodology
The Cambridge Serial Total Energy Package (CASTEP)29 was used. To encounter the effect of localized electrons and bandgap underestimation we employed the hybrid functional PBE0 with norm conserving pseudopotentials30. Convergence tests revealed that a cutoff energy was chosen of 800 eV and 2 × 2 × 3 k-points for the sampling of the Brillouin zone were sufficient for the 48 atom supercell (2 × 2 × 2 unit cells). The supercell was chosen by taking into account that although hybrid functionals can provide more reliable results, they are very computationally expensive. For the optimization of the relaxed structures and the prediction of the ground state of each system, we used the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method which was seen to predict the correct ground state to various different system31. For the interstitial positions we examined all possible configurations in the supercell in conjunction with geometry optimization and retained the lowest energy configuration. Specifically, we placed the interstitial defects in various sites and we used as the final ground state the configuration with the minimum total energy. The surface simulation was based on a slab model with a vacuum of about 12 Å vertical to the (110) direction. Here, the top two layers represent the surface, whereas the bottom two layers are fixed and represent the bulk region. Considering the DOS calculations a k-point mesh of 5 × 5 × 5 was used for bulk and 3 × 3 × 1 set for the surface. We set the convergence criteria at 2.0 × 10−5 eV/atom for the SCF tolerance, 0.05 eV/Å for the force tolerance and 0.001 Å for the max displacement tolerance.
Results and discussion
Bulk SnO2
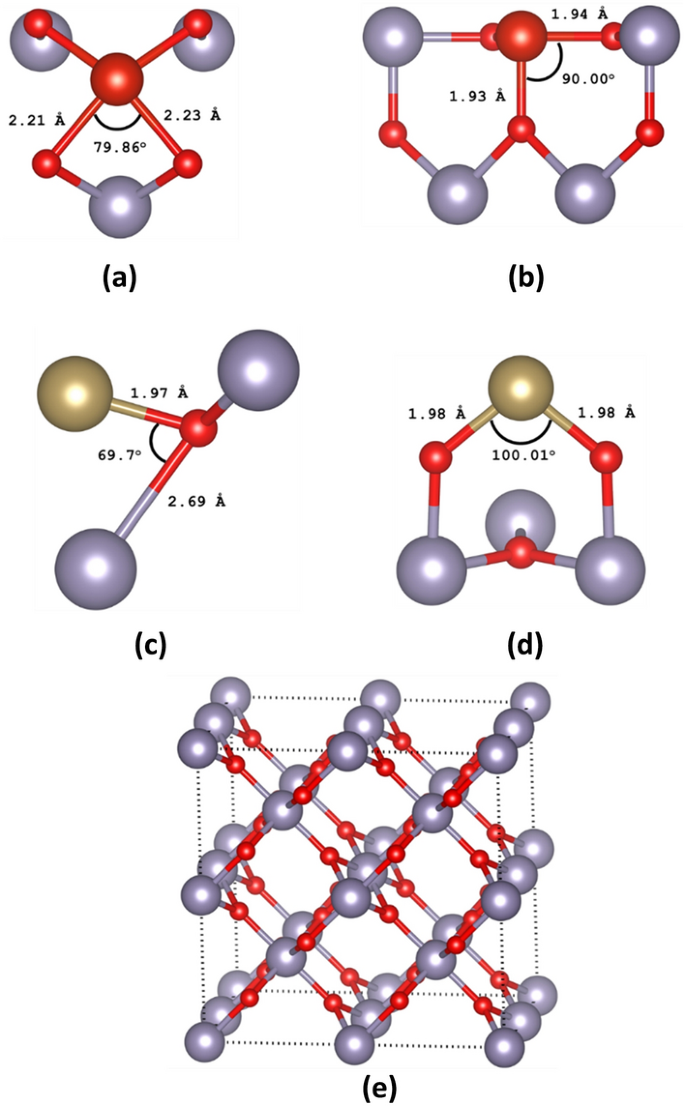
Here we considered SnO2 in the rutile structure (space group number P42/mmm), with determined unit cell parameters a = b = 4.737 Å and c = 3.186 Å and our DFT calculated unit cell parameters are a = b = 4.717 Å and c = 3.189 Å14. In Fig. 1, we report the minimum energy configurations with relevant nearest neighbour distances and angles of (a) Ta substitutional doped SnO2 (TaSn:SnO2), (b) Ta interstitial doped SnO2 (Tai:SnO2), (c) V substitutional doped SnO2 (VSn:SnO2), (d) V interstitial doped SnO2 (Vi:SnO2) and (e) the undoped 48-atom supercell. We have considered all the possible configurations of these defects in the supercell but the subsequent figures report results on the minimum energy configurations only.

The minimum energy configurations of (a) Ta substitutional doped SnO2 (TaSn:SnO2), (b) Ta interstitial doped SnO2 (Tai:SnO2), (c) V substitutional doped SnO2 (VSn:SnO2), (d) V interstitial doped SnO2 (Vi:SnO2) and (e) the supercell.
In Table 1 we have gathered the lattice parameters for all the doping cases. As it is seen, in all the cases except the vanadium substitutional, the volume of the unit cell increases. Typically, a larger supercell is connected to larger area for the chemical reactions to take place and can lead to improved photocatalytic activity of SnO2. Our approach agrees well with experimental reports23,32. Specifically, Alvarez-Roca et al.23 investigated at various vanadium doping concentration the X-ray diffraction and transmittance electron microscope for the determination of the structural changes in SnO2. Similar to our study, the found that the V atoms can be incorporated inside the structure of SnO2 and at low concentrations the cell volume is reduced. According to their study, this reduction enhances the specific surface area to volume ration which is highly beneficial for applications of V:SnO2 in catalysis, sensors and energy applications. Continuing with the recent work of Uwihoreye et al.32, where they investigated the structural, electronic and optical properties of Ta:SnO2 thin films, they found that at low Ta concentrations, the lattice parameters of SnO2 are slightly reduced with the volume remaining almost unchanged. At low concentrations the incorporation of Ta atoms takes place in Sn sites and due to the smaller radius of Ta atoms (0.064 nm) compared to Sn atoms (0.065 nm) this leads to relative decrease of the lattice parameters. As they report, at higher concentration this phenomenon is reversed and the volume is increased. We believe that this is happening because at higher concentrations it is more likely for interstitials to form, and as we show, Tai:SnO2 exhibits a higher volume than TaSn:SnO2. While our work predicts similar trends with the above mentioned experimental works, in order to explain completely and with great accuracy the above mentioned experimental results, different doping concentration should be examined, which is beyond of the scope of this paper. Ali and Islam33 investigated using DFT the effect of Ta doping in SnO2 and they also predicted that incorporation of Ta in SnO2 increases the volume of the supercell.
Continuing our work with the electronic investigation of Ta/V doped SnO2 we report in Fig. 2 the calculated total DOS and the (partial) PDOS for each doping case. As it is shown in Fig. 2e, the hybrid functional DFT calculations using PBE0 result in a bandgap value of 3.35 eV13, in excellent agreement with the experimentally determined bandgap23. Doping with Tai or Vi will result in a small increase of the band gap, however Ta and V at substitutional sites reduce the band gap by about 0.5 eV (refer to Table 2). Overall, The decrease of the band gap for the V and Ta doping, is caused by the overlapping of V-3d (Ta-3d) with O-2p. Those overlapping could initiate the formation not only of states near the band edges but also of intermediate bands (deep states). The increase of the bandgap in Tai could be attributed to the effect of electron doping which is responsible for shifting the fermi level into the conduction band, this phenomenon is also called Burstein-Moss effect34.

The total DOS and the projected density of states (PDOS) of (a) Vi:SnO2, (b) VSn:SnO2, (c) Tai:SnO2 (d) TaSn:SnO2, and (e) undoped SnO2.
For both Vi:SnO2 (Fig. 2a) and Tai:SnO2 (Fig. 2c) in gap states form to the conduction band edge and the bandgap calculated to increase to 3.39 eV and 3.48 eV, respectively (Table 2). This formation of energy states in the middle of the bandgap can be advantageous for photocatalytic applications, however it is detrimental for photovoltaics and light emission diodes as they act as traps that reduce the device photocurrent and photogenerated charge carriers. Conversely, for VSn:SnO2 (Fig. 2b) and TaSn:SnO2 (Fig. 2d) the band gap is reduced to 2.86 eV and 2.84 eV, respectively (refer to Table 1). This band gap reduction is attractive for photocatalytic applications.
Figure 3 reports the refractive index with respect the phonon energy for all the doping cases considered. For zero frequency the refractive index is predicted to be a 1.40, in excellent agreement with previous theoretical studies but lower as compared to the experimental value (1.70)35,36. From Table 2 and Fig. 3 it is clear that there is an increase for the lower photon energies and a decrease in the upper energies.

The refractive index for (a) Vi:SnO2, (b) VSn:SnO2, (c) Tai:SnO2 and (d) TaSn:SnO2. The dotted purple and dotted green, correspond to the dielectric function of the undoped SnO2.
Figure 4 reports the reflectivity (i.e. amount of photons that are reflected) and it is predicted that Vi:SnO2 has the highest reflectivity in the near-infrared region (refer to Table 2). Ta-doped SnO2 has low reflectivity in the infrared and visible region therefore it can be used as an antireflective coating.

The reflectivity of the doped structures. The dotted purple line corresponds to undoped SnO2.
In Fig. 5a,b present the optical conductivity and absorption coefficient for all the doping cases considered here. The optical conductivity is effectively represented by the mobility of excitons (electron–hole pairs) a crucial parameter in the design of optical detectors37. The excitons are generated when photons have higher energy than the optical bandgap and because of the electronic charge neutrality do not contribute to the electrical conductivity38. The absorption of undoped SnO2 starts at 380 nm in fair agreement with the experimental value (400 nm)39. From Fig. 5b it is observed that that Tai and Vi have the highest absorption in the visible region.

(a) The optical conductivity with respect to the photon energy and (b) the absorption coefficient with respect to the wavelength for the investigated dopants.
Surface SnO2
The investigation of the most exposed surface, in this case the (110) surface13, is of crucial importance for the application of doped SnO2 to various technologies such as gas sensors40 and photocatalytic hydrogen production41. Specifically for the gas sensors the adsorption and desorption of oxygen and gas molecules occurs on the surfaces of the material while for the hydrogen production the most high-energetic surface will play the role of the active site in photocatalytic reactions. As it is seen from the available literature, the studies of the (110) SnO2 surface are significantly less compared to the studies of the bulk.
In this section, the electronic density of states changes of the undoped and the V. Ta doped SnO2 were investigated. The (110) surface is cleaved from the bulk SnO2 and it is represented with a nine-layer slab model, as it is presented in Fig. 6. The (110) surface consists of 16 SnO2 atoms and 32 O atoms while the size of the vacuum is chosen at 12 Å. For our calculations the bottom 4 layers are kept fixed during the geometry optimization in order to represent the bulk side while the top 5 are free to relax for the energy minimization. Our model has been used to various other studies, such as were the adsorption of hydrogen molecules on Cu-doped SnO2 surface is chosen42. Similarly, the same process was followed in this paper in order to simulate the minimum energy system for the doped surface. Furthermore, to accurate predict the DOS characteristics the hybrid functional PBE0 was used.

The slab model used for the V, Ta doped SnO2.
The total Density of states of the undoped and the V,Ta-doped SnO2 surface, as well as the partial density of states of O, Sn, V and Ta atom as are depicted in Fig. 7a–c. From our results in Fig. 7a it can be seen that V doping produces a surface band gap of nearly 2 eV. Compared to the pure SnO2 (110) facet it can be observed that the valence band is increased after V doping as some additional states are created at 0.5 eV. Our analysis shows that V doping reduces the bandgap of approximately 0.5 eV. Moreover, additional states are created at the conduction band edge. Continuing with the Ta doping, it can be observed that the bandgap is reduced to a value equal to 1.8 eV while the only energy states that arise are located at 1 eV. Compared to the undoped, Ta doping reduces the bandgap nearly 0.7 eV.

The total density of states (DOS) and the projected density of states (PDOS) of (a) V, (b) Ta and (c) undoped (110) SnO2 facet.
From the surface simulations it can be concluded that gap states that serve as electron traps are formed near the conduction band in all the doping cases. As these trap states are of great importance for the gas sensors and photocatalysis and so further experimental investigation is suggested.
Conclusions
In the present DFT investigation the structural, electronic and optical properties of V and Ta doped SnO2 were calculated. Our first principles studies investigated the potential of these doping techniques for energy and sensing applications as it involved advanced hybrid calculations both for the bulk and the surface of SnO2. The DOS calculations revealed that there is a small bandgap increase for Tai and Vi doping, whereas for both the Ta and V substitutionals, the bandgap is decreased. Our calculations for the bulk agree well with other experimental reports and explain the trends that could be seen in them. The reduction of the band gap in the substitutional cases and the mid-gap states for the interstitial cases can be beneficial for photocatalytic applications while when the band gap is increased especially in the Vi case this can be beneficial for other applications such as electron transport layers. Furthermore, surface calculations indicate that these systems can be applicable for gas sensors as they can provide active sites for the sensing reactions to take place and also the gap states formed can further enhance these reactions. Therefore experimental work is necessary.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
-
Fortunato, E., Ginley, D., Hosono, H. & Paine, D. C. Transparent conducting oxides for photovoltaics. MRS Bull. 32, 242–247 (2007).
Google Scholar
-
Mallikarjuna, K., Rafiqul Bari, G. A. K. M., Vattikuti, S. V. P. & Kim, H. Synthesis of carbon-doped SnO2 nanostructures for visible-light-driven photocatalytic hydrogen production from water splitting. Int. J. Hydrog. Energy 45, 32789–32796 (2020).
Google Scholar
-
Trani, F., Causà, M., Ninno, D., Cantele, G. & Barone, V. Density functional study of oxygen vacancies at the SnO2 surface and subsurface sites. Phys. Rev. B 77, 245410 (2008).
Google Scholar
-
Villamagua, L. et al. Change in the electrical conductivity of SnO2 crystal from n-type to p-type conductivity. Chem. Phys. 452, 71–77 (2015).
Google Scholar
-
Isono, T. et al. Highly conductive SnO2 thin films for flat-panel displays. J. Soc. Inf. Disp. 15, 161 (2007).
Google Scholar
-
Robertson, J. High dielectric constant gate oxides for metal oxide Si transistors. Rep. Prog. Phys. 69, 327–396 (2006).
Google Scholar
-
Zunger, A., Kilic, C. & Wang, L. Defects in photovoltaic materials and the origin of failure to dope them. in Conference Record of the Twenty-Ninth IEEE Photovoltaic Specialists Conference, 2002 500–503 (IEEE, 2002). https://doi.org/10.1109/PVSC.2002.1190611
-
Vasilopoulou, M. et al. Charge transport materials for mesoscopic perovskite solar cells. J. Mater. Chem. C 10, 11063–11104 (2022).
Google Scholar
-
Zhou, W., Liu, Y., Yang, Y. & Wu, P. Band gap engineering of SnO2 by epitaxial strain: Experimental and theoretical investigations. J. Phys. Chem. C 118, 6448–6453 (2014).
Google Scholar
-
Batzill, M. & Diebold, U. The surface and materials science of tin oxide. Prog. Surf. Sci. 79, 47–154 (2005).
Google Scholar
-
Le Corre, V. M. et al. Charge transport layers limiting the efficiency of perovskite solar cells: How to optimize conductivity, doping, and thickness. ACS Appl. Energy Mater. 2, 6280–6287 (2019).
Google Scholar
-
Filippatos, P.-P., Kelaidis, N., Vasilopoulou, M., Davazoglou, D. & Chroneos, A. Defect processes in halogen doped SnO2. Appl. Sci. 11, 551 (2021).
Google Scholar
-
Filippatos, P.-P., Kelaidis, N., Vasilopoulou, M., Davazoglou, D. & Chroneos, A. Impact of boron and indium doping on the structural, electronic and optical properties of SnO2. Sci. Rep. 11, 13031 (2021).
Google Scholar
-
Zhang, P., Hong, R. Y., Chen, Q. & Feng, W. G. On the electrical conductivity and photocatalytic activity of aluminum-doped zinc oxide. Powder Technol. 253, 360–367 (2014).
Google Scholar
-
Menil, F., Lucat, C. & Debeda, H. The thick-film route to selective gas sensors. Sens. Actuators B Chem. 25, 415–420 (1995).
Google Scholar
-
Ivanov, P. et al. Development of high sensitivity ethanol gas sensors based on Pt-doped SnO2 surfaces. Sens. Actuators B Chem. 99, 201–206 (2004).
Google Scholar
-
Barbosa, M. S. et al. Gas sensor properties of Ag- and Pd-decorated SnO micro-disks to NO2, H2 and CO: Catalyst enhanced sensor response and selectivity. Sens. Actuators B Chem. 239, 253–261 (2017).
Google Scholar
-
Lin, Y. et al. Synergistically improved formaldehyde gas sensing properties of SnO2 microspheres by indium and palladium co-doping. Ceram. Int. 41, 7329–7336 (2015).
Google Scholar
-
Kim, H.-J. & Lee, J.-H. Highly sensitive and selective gas sensors using p-type oxide semiconductors: Overview. Sens. Actuators B Chem. 192, 607–627 (2014).
Google Scholar
-
Rajeshwaran, P. & Sivarajan, A. Influence of Mn doping on structural, optical and acetone gas sensing properties of SnO2 nanoparticles by a novel microwave technique. J. Mater. Sci. Mater. Electron. 26, 539–546 (2015).
Google Scholar
-
Bagwasi, S., Tian, B., Zhang, J. & Nasir, M. Synthesis, characterization and application of bismuth and boron Co-doped TiO2: A visible light active photocatalyst. Chem. Eng. J. 217, 108–118 (2013).
Google Scholar
-
Kou, X. et al. Synthesis of Co-doped SnO2 nanofibers and their enhanced gas-sensing properties. Sens. Actuators B Chem. 236, 425–432 (2016).
Google Scholar
-
Alvarez-Roca, R., Desimone, M., Da Silva, M. G. S., Ponce, M. A. & Longo, E. Vanadium doping effect on multifunctionality of SnO2 nanoparticles. J. Mater. Appl. 9, 38–45 (2020).
Google Scholar
-
Slassi, A. Ab initio study on the structural, electronic, optical and electrical properties of Mo-, Nb- and Ta-doped rutile SnO2. Opt. Quantum Electron. 48, 160 (2016).
Google Scholar
-
Maleki, M. Ab initio calculations of the effect of N, Nb, and Ta doping on the electronic structure and optical properties of SnO2. J. Comput. Electron. 19, 47–54 (2020).
Google Scholar
-
Williamson, B. A. D. et al. Resonant Ta doping for enhanced mobility in transparent conducting SnO2. Chem. Mater. 32, 1964–1973 (2020).
Google Scholar
-
Liu, Q. et al. Effect of tantalum doping on SnO2 electron transport layer via low temperature process for perovskite solar cells. Appl. Phys. Lett. 115, 143903 (2019).
Google Scholar
-
Soltan, W. B., Lassoued, M. S., Ammar, S. & Toupance, T. Vanadium doped SnO2 nanoparticles for photocatalytic degradation of methylene blue. J. Mater. Sci. Mater. Electron. 28, 15826–15834 (2017).
Google Scholar
-
Segall, M. D. et al. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 14, 2717–2744 (2002).
Google Scholar
-
Paier, J. et al. Screened hybrid density functionals applied to solids. J. Chem. Phys. 124, 154709 (2006).
Google Scholar
-
Qureshi, M. W. et al. Verification of stability and unraveling the electronic and physical properties of bulk and (001)-surfaces of newly synthesized Ti2ZnX (X = C, N) MAX phases. Surf. Interfaces 31, 102032 (2022).
Google Scholar
-
Uwihoreye, V. et al. Transparent conductive SnO2 thin films via resonant Ta doping. Sci. China Mater. 66, 264–271 (2023).
Google Scholar
-
Ali, M. A. & Islam, A. K. M. A. Sn1−xBixO2 and Sn1−xTaxO2 (0 ≤ x ≤ 0.75): A first-principles study. Phys. B Condens. Matter 407, 1020–1026 (2012).
Google Scholar
-
Turgut, G. Effect of Ta doping on the characteristic features of spray-coated SnO2. Thin Solid Films 594, 56–66 (2015).
Google Scholar
-
Afify, H. H., Momtaz, R. S., Badawy, W. A. & Nasser, S. A. Some physical properties of fluorine-doped SnO2 films prepared by spray pyrolysis. J. Mater. Sci. Mater. Electron. 2, 40–45 (1991).
Google Scholar
-
Khan, A. F., Mehmood, M., Aslam, M. & Ashraf, M. Characteristics of electron beam evaporated nanocrystalline SnO2 thin films annealed in air. Appl. Surf. Sci. 256, 2252–2258 (2010).
Google Scholar
-
Akinlami, J. O. & Olateju, I. O. Reflection coefficient and optical conductivity of gallium nitride GaN. Semicond. Phys. Quantum Electron. Optoelectron. 15, 281–284 (2012).
Google Scholar
-
Dash, L. K., Vast, N., Baranek, P., Cheynet, M.-C. & Reining, L. Electronic structure and electron energy-loss spectroscopy of ZrO2 zirconia. Phys. Rev. B 70, 245116 (2004).
Google Scholar
-
Doyan, A., Susilawati, S. & Imawanti, Y. D. Synthesis and characterization of SnO2 thin layer with a doping aluminum is deposited on quartz substrates. AIP Conf. Proc. 1801, 020005. https://doi.org/10.1063/1.4973083 (2017).
Google Scholar
-
Filippatos, P.-P. et al. Optimization of the hydrogen response characteristics of halogen-doped SnO2. Sci. Rep. 13, 2524 (2023).
Google Scholar
-
Talebian, N. & Jafarinezhad, F. Morphology-controlled synthesis of SnO2 nanostructures using hydrothermal method and their photocatalytic applications. Ceram. Int. 39, 8311–8317 (2013).
Google Scholar
-
Wang, F. et al. Adsorption mechanism of Cu-doped SnO2 (110) surface toward H2 dissolved in power transformer. J. Nanomater. 2016, 1–9 (2016).
Google Scholar
Acknowledgements
The open access fee was paid from the Imperial College London Open Access Fund.
Author information
Authors and Affiliations
Contributions
P.P.F. performed the calculations, P.P.F. and A.C. wrote the main manuscript. All authors contributed and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and Permissions
About this article
Cite this article
Filippatos, PP., Kelaidis, N., Vasilopoulou, M. et al. Vanadium and tantalum doping of tin dioxide: a theoretical study.
Sci Rep 13, 20983 (2023). https://doi.org/10.1038/s41598-023-47383-3
-
Received: 07 August 2023
-
Accepted: 13 November 2023
-
Published: 28 November 2023
-
DOI: https://doi.org/10.1038/s41598-023-47383-3
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.