Solving partial differential equations (PDEs) with numerical methods has a pivotal role in a wide variety of disciplines in science and engineering, with applications such as topology and design optimization¹ and clinical prognostication². Although effective, numerical methods can be computationally intensive or even prohibitive due to performing multiple independent PDE approximations on families of geometries and with multiple initial and boundary conditions. Thus, developing techniques that aim at improving efficiency by exploiting relationships between solutions over different geometries and initial and boundary conditions is a task of substantial importance.

Within the emerging field of scientific machine learning, many artificial intelligence approaches have been proposed to approximate the PDE solutions. The idea of solving PDEs with neural networks can be traced back to at least the 1990s^3,4, and has received much attention in the past decade due to the advance in computational ability for training deep neural networks^5,6,7,8. In particular, using artificial intelligence to learn the PDE solution operator, termed neural operator, is of particular interest as it enables approximating PDE solutions with varying boundary and initial conditions, and over parametric families of PDEs (for example, modeling local material properties^9,10).

Despite its success, the computational bottleneck when performing tasks in optimization and prognostication still exists due to the inability of neural operators to estimate geometry-dependent PDE solutions. Most current frameworks for neural operators are formulated on a domain with fixed boundaries, and variations in the shape of the learning domain require retraining the neural network. Previous attempts to extend the learning ability to various geometries adopted approaches based on transformer architecture^11,12,13, neural fields¹⁴, graph encoding¹⁵ and convolutional neural networks¹⁶, among others¹⁷. The main challenge of learning geometry-dependent operators emanates from the scalability of learning on three-dimensional (3D) geometries with complex shapes. Furthermore, the generic formulation and the approximation theorem of neural operators on a family of Banach spaces over various domains have not been established yet.

Here we aim to address the aforementioned computational challenges by proposing Diffeomorphic Mapping Operator Learning (DIMON), an operator learning framework that enables scalable geometry-dependent operator learning on a wide family of diffeomorphic domains. DIMON combines neural operators with diffeomorphic mappings between domains and shapes, formulating the learning problem on a unified reference domain (‘template’) Ω⁰, but with respect to a suitably modified PDE operator. PDE solutions along with input functions on a family of diffeomorphically equivalent shapes are each mapped onto the reference domain Ω⁰ via a diffeomorphism, which essentially transports functions from a family of Banach spaces to a single space and provides a unified framework for approximation analysis. This map can also be interpreted as a change of variables in the PDE on the original shape, yielding a corresponding PDE on Ω⁰, parameterized by the diffeomorphism and geometry. Then, a neural operator is trained to learn the latent solution operator of this parameterized and geometry-dependent PDE on Ω⁰, where the parameter that encodes the shape of the original domain represents the diffeomorphic mapping. We propose to compress the mapping in a suitable way to reduce both the dimension of the input space of the network and the computational cost of training the neural network, hence facilitating the network scalability on learning from PDE systems on 3D shapes. The original operator is equivalent to the composition of the learned modified operator on the reference domain with the inverse of the diffeomorphism from the original domain. Thereby, learning the geometry-dependent, parameterized PDE operators on the reference domain yields an efficient way of solving PDEs on a family of domains.

The idea of learning geometry-dependent operators by combining diffeomorphism with neural operators, albeit quite natural, is theoretically sound and flexible. To demonstrate DIMON’s utility, we further extend the universal approximation theorem¹⁸ and show that the latent operator on Ω⁰ can be approximated by adopting a multiple-input operator (MIONet). In addition, DIMON is flexible with the choice of diffeomorphic mapping algorithms, reference domains Ω⁰ and approaches for geometry parameterization^19,20,21, and it poses no constraints on choosing the architecture of neural operators. Moreover, we demonstrate the learning ability and efficiency of DIMON with three examples that include learning diverse types of static and dynamic PDE problems on both parameterized and non-parameterized domains. At the inference stage, DIMON reduces the wall time needed for predicting the solution of a PDE on an unseen geometry by a factor of up to 10,000 with substantially less computational resources and high accuracy. In particular, the last example approximates functionals of PDE solutions (in fact, PDEs couple with a rather high-dimensional ordinary differential equations system) for determining electrical wave propagation on thousands of personalized heart digital twins, demonstrating its scalability and utility in learning on realistic 3D shapes and dynamics in precision medicine applications.

Method overview

This section provides an overview of DIMON.

Problem formulation

In this section, we present the formulation of DIMON for learning operators on a family of diffeomorphic domains, along with the unfolding of how a pedagogical example problem is set up and solved.

Set-up

Consider a family ({{{varOmega }^{theta }}}_{theta in varTheta }) of bounded, open domains with Lipschitz boundaries in ({{mathbb{R}}}^{d}), with Θ a compact subset of ({{mathbb{R}}}^{p}). d is the dimension of boundaries and p is the dimension of parameter set. Assume that for each shape parameter θ ∈ Θ there is a ({{mathcal{C}}}^{2}) embedding φ_θ from the ‘template’ Ω⁰ to ({{mathbb{R}}}^{d}), which induces a ({{mathcal{C}}}^{2}) diffeomorphism (that is a bijective ({{mathcal{C}}}^{2}) map with ({{mathcal{C}}}^{2}) inverse) between Ω⁰ and Ω^θ. We further assume that the map (varTheta to {{mathcal{C}}}^{2}({varOmega }^{0},{{mathbb{R}}}^{d})), defined by θ ↦ φ_θ is continuous, when ({{mathcal{C}}}^{2}) is endowed with the usual ({{mathcal{C}}}^{2}) norm that makes it a Banach space. Assume that for each θ ∈ Θ there is a solution operator ({{mathcal{G}}}_{theta }:{X}_{1}({varOmega }^{theta })times ldots {X}_{m}({varOmega }^{theta })to Y({varOmega }^{theta })) mapping functions ({v}_{1}^{theta },ldots ,{v}_{m}^{theta }) on Ω^θ or ∂Ω^θ, representing a set of initial and boundary conditions, to the solution u^θ(*; v^θ) on Ω^θ of a fixed PDE, where ({{bf{v}}}^{theta }:= ({v}_{1}^{theta },ldots ,{v}_{m}^{theta })). X₀, X₁ …, X_m, Y are Banach spaces.

We may represent this family ({{{{mathcal{G}}}_{theta }}}_{theta in varTheta }) of operators defined on functions on different domains by an operator ({{mathcal{F}}}_{0}) dependent on the shape parameter θ and on functions that are all defined on the reference domain Ω⁰, by suitable compositions with the diffeomorphisms φ_θ and ({varphi }_{theta }^{-1}), as follows:

where the second equality defines ({{mathcal{F}}}_{0}), the third equality defines ({v}_{k}^{0}:= {v}_{k}^{theta }circ {varphi }_{theta }), and the fourth equality shows that ({u}_{theta }^{0}(* ;{{bf{v}}}_{theta }^{0}):= {u}^{theta }(* ;{{bf{v}}}^{theta })circ {varphi }_{theta }). The ‘latent’ geometry-dependent operator ({{mathcal{F}}}_{0}:varTheta times {X}_{1}({varOmega }^{0})times)(cdots times {X}_{m}({varOmega }^{0})to Y({varOmega }^{0})) maps θ ∈ Θ and a set of functions ({v}_{k}^{0}) in some Banach Spaces (({X}_{k}({varOmega }^{0}),| | * | {| }_{{X}_{k}({varOmega }^{0})})), for k = 1, …, m, of functions on Ω⁰ or ∂Ω⁰, to a target function ({u}_{theta ,{{bf{v}}}^{0}}^{0}) in a Banach Space ((Y({varOmega }^{0}),| | * | {| }_{Y({varOmega }^{0})})) of functions over Ω⁰. As above, we used the vector notation v⁰ to denote (({v}_{1}^{0},ldots ,{v}_{m}^{0})). One can view ({{mathcal{F}}}_{0}) as the operator that outputs the pullback of a solution of a PDE on Ω^θ to the reference domain Ω⁰ via the diffeomorphism φ_θ; this is analogous to the Lagrangian form of the solution operator in contrast with the Eulerian form ({{mathcal{G}}}_{theta }) defined on the varying domain using the terminology in ref. ²².

Learning problem

Given N observations (left{left({varOmega }^{{theta }_{i}},{v}_{1}^{{theta }_{i}}ldots ,{v}_{m}^{{theta }_{i}},right.right.)(left.left.{{mathcal{G}}}_{{theta }_{i}}({v}_{1}^{{theta }_{i}},ldots ,{v}_{m}^{{theta }_{i}})right)right}_{i = 1}^{N}) and a diffeomorphism φ_θ, where θ_i and ({v}_{k}^{{theta }_{i}}) are all independently sampled at random from a probability measure on Θ and on compact subsets of X_k, respectively, we aim at constructing an estimator of ({{mathcal{F}}}_{0}) defined in equation (1).

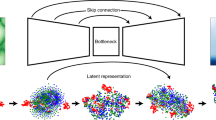
We choose the estimator in the form of a neural operator ({tilde{{mathcal{F}}}}_{0}), which takes as inputs the shape parameter θ, the transported input functions ({{bf{v}}}_{theta }^{0}), and outputs an approximation to ({{mathcal{F}}}_{0}(theta ,{{bf{v}}}_{theta }^{0})). We visualize the framework in Fig. 1a and the high-level architecture of the neural operator in Fig. 1b; we discuss more details of the neural operator and its approximation ability in the following section.

a, A partial differential operator ({{mathcal{G}}}_{theta }) is posed on ({varOmega }^{{theta }_{i}}) together with functions ({{bf{v}}}^{{theta }_{i}}(i=1,ldots ,N)) as input. A map φ_θ, parameterized by the shape parameter θ, transports ({{bf{v}}}_{theta }^{0}) posed on reference domain Ω⁰ onto Ω^θ and identifies point correspondences across all Ω^θ and Ω⁰ (indicated by red marks and blue dots). There exists a latent operator ({{mathcal{F}}}_{0}) such that ({{mathcal{G}}}_{theta }({{bf{v}}}^{theta })={{mathcal{F}}}_{0}(theta ,{{bf{v}}}_{theta }^{0})circ {varphi }_{theta }^{-1}). b, The operator ({{mathcal{F}}}_{0}) is approximated by a neural operator ({tilde{{mathcal{F}}}}_{0}): a shape parameter θ (typically estimated from data) and the transported function (or Func.) ({{bf{v}}}_{theta }^{0}) are the inputs of branch networks; the coordinates of the reference domain x are the inputs of the trunk network.

Full size image

The framework discussed above extends immediately to at least the following settings:

• Time-dependent operators, by concatenating time t to coordinate x (see example 2).

• Operators that involve vector- or tensor-valued functions, by replacing the pullback operation on scalar functions with an appropriate action of diffeomorphisms on the vector and tensor fields. For example, the action of φ_θ on a vector field (v:{varOmega }^{0}to {{mathbb{R}}}^{d}) is the vector field defined for all x_θ = φ_θ(x) ∈ Ω^θ by: Jφ_θ ⋅ v(x), where Jφ_θ denotes the Jacobian matrix of the transformation. This action can be further extended to covariant/contravariant tensor fields of any type.

Universal approximation theorem on a diffeomorphic family of domains

In this section, we extend the applicability of the universal approximation theorem (UAT) presented in ref. ¹⁸ on learning parametric domains for multi-input operators under the DIMON framework. In short, the UAT in ref. ¹⁸ guarantees the approximation ability of a multi-branch DeepONet for nonlinear and continuous operators with the assumption of fixed domains. Transporting functions defined on various domains via φ_θ onto a reference domain with a fixed boundary naturally aligns well with the assumption of UAT, hence enabling learning on various domains. To differentiate the mapping φ and the shape of Ω^θ, we define a shape parameter θ ∈ Θ ⊂ X₀ in a Banach space X₀ and introduce the branch for encoding geometric information, referred to as Geo. branch. Therefore, the adapted UAT can be written as:

Theorem 1

(Adapted from ref. ¹⁸.) Assume that X₀, X₁ …, X_m, Y are Banach spaces, Θ ⊂ X₀, K_i ⊂ X_i (i = 1, …, m) are compact sets, and X_i (i = 0, …, m) has a Schauder basis. If ({{mathcal{F}}}_{0}:varTheta times {K}_{1}times cdots times {K}_{m}to Y) is a continuous operator, then for any ϵ > 0, there exists a neural network (tilde{{{mathcal{F}}}_{0}}) with the form given in equation (8), such that

where the norm C is the sup norm, K_i are compact sets as shown in the theorem and ϵ is a positive number.

Despite its generality, the use of Theorem 1 for the approximation of solution operators of PDEs typically requires extra analysis, in particular to ensure that the assumptions on ({{mathcal{F}}}_{0}) are satisfied, namely, the well posedness and continuity with respect to the domain geometry as well as initial and boundary conditions: this can be non-trivial for many PDEs. While it is out of the scope of the present paper to discuss this in a systematic fashion, we detail below and in Supplementary Information the particular case of the Laplace equation introduced above, under suitable regularity assumptions.

Although we chose a particular MIONet as the baseline neural operator model in this work, DIMON is agnostic to the choice of neural operators. This flexibility allows one to seamlessly integrate between previous endeavors in neural operators^{9,10,12,23,24} and DIMON in a plug-and-play fashion.

Illustrative example

Let us consider the problem of solving the Laplace equation on a family of bounded open domains ({{{varOmega }^{theta }}}_{theta in varTheta }) of ({{mathbb{R}}}^{2}) with Lipschitz regular boundaries, where Θ is a compact subset of ({{mathbb{R}}}^{p}). We assume that Ω^θ is, for each θ ∈ Θ, diffeomorphic to a fixed domain ({varOmega }^{0}subset {{mathbb{R}}}^{2}), which we call the reference domain. For example, if Ω^θ is a simply connected domain for each θ, Ω⁰ may be chosen to be the open unit disk ({xin {{mathbb{R}}}^{d},:,| | x| {| }_{2} < 1}), and φ_θ smooth (in fact, holomorphic if ({{mathbb{R}}}^{2}) is identified with ({mathbb{C}})) bijection of Ω^θ onto Ω⁰ exists by the Riemann mapping theorem.

For each θ ∈ Θ, we are interested in obtaining the solution of the PDE

for ({v}_{1}^{theta }) a function on ∂Ω^θ with ({v}_{1}^{theta }in {H}^{frac{1}{2}}(partial {varOmega }^{theta })), where H^s is the standard Sobolev space of order s, and with the boundary conditions intended in the trace sense. In this setting, it is known that there exists a unique weak solution ({u}^{theta }(* ;{v}_{1}^{theta })in {H}^{1}({varOmega }^{theta })) to this boundary problem, compare, for instance, in ref. ²⁵ or ref. ²⁶. We are interested in learning the solution operator ({{mathcal{G}}}_{theta }({v}_{1}^{theta }):= {u}^{theta }(* ;{v}_{1}^{theta })) for this Laplace equation over the various domains Ω^θ with boundary conditions ({v}_{1}^{theta }).

The operator ({{mathcal{F}}}_{0}) to approximate maps a shape parameter θ and boundary function ({v}_{1}^{theta }) to the (weak) solution of equation (2) pulled back on the template domain Ω⁰. Formally, denoting ({u}_{theta }^{0}(* ;{v}_{theta }^{0})={{mathcal{F}}}_{0}(theta ,{v}_{theta }^{0})), where ({v}_{theta }^{0}={v}_{1}^{theta }circ {varphi }_{theta },{u}_{theta }^{0}(* ;{v}_{theta }^{0})) can be equivalently viewed as the solution of a uniformly elliptic Dirichlet problem on Ω⁰, namely

in which ({varphi }_{theta }^{* }) denotes the operator mapping an arbitrary function h on Ω_θ to the function h ∘ φ_θ on Ω⁰. Note that the specific coefficients of this linear second-order elliptic operator ({L}_{theta }={varphi }_{theta }^{* },Delta ,{({varphi }_{theta }^{-1})}^{* }) could be written explicitly based on the first and second-order derivatives of φ_θ, and are in particular continuous functions on Ω⁰, compare in Supplementary Section 1 for more details.

The key issue to apply Theorem 1 in this case is to determine adequate functional spaces for the solution and boundary function under which ({u}_{theta }^{0}(cdot ;{v}_{theta }^{0})) is first well defined but also continuous with respect to ({v}_{theta }^{0}) and θ. The existence and uniqueness of weak solutions in H¹(Ω⁰) for smooth domains and ({v}_{theta }^{0}in {H}^{frac{1}{2}}(partial {varOmega }^{0})) follow from classical results on elliptic PDEs (Ch. 8 in ref. ²⁵), and have been extended to Lipschitz regular domains in ref. ²⁶. Well-developed regularity estimates for this class of PDEs also guarantee the continuity of the solution with respect to the boundary function ({v}_{theta }^{0}). However, to our knowledge, regularity with respect to domain deformations (and thus θ) is much less well understood in such a general setting. On the basis of the continuity of the mapping θ ↦ φ_θ from Θ to ({{mathcal{C}}}^{2}({varOmega }^{0},{{mathbb{R}}}^{d})) and by adapting the ideas presented in ref. ²², one can recover the solution’s continuity with respect to θ albeit under the stronger assumption that Ω⁰ has a ({{mathcal{C}}}^{2}) boundary; see Supplementary Section 1 for additional details. With such assumptions, the conclusion of Theorem 1 holds and it is thus possible to approximate the solution operator up to any precision using the operator learning framework developed in this paper.

Algorithms and practical considerations

In practice, the domain Ω^θ may be available only in discretized form, and numerical methods are used to approximate the solution of a PDE on the domain of Ω^θ. For all the examples presented in this work, we adopt a finite element method (FEM) with a piece-wise linear basis to generate a training set of PDE solutions, consistent with the assumption u^θ ∈ H¹(Ω^θ) on the weak solution. One could adopt numerical methods with higher-order polynomials, such as spectral element methods^27,28 or hp-FEM²⁹, to approximate smoother PDE solutions with higher accuracy; note that in this case, the differentiability of φ_θ needs to be sufficiently high to preserve the smoothness solution after composition.

Choosing the reference domain Ω
⁰

In general, there is no canonical choice for Ω⁰, or for the diffeomorphisms between Ω⁰ and Ω^θ. Often the domains are unparameterized, given, for instance, meshes with no explicit point correspondences between them. For such unparameterized domains, a practical choice is then to set a reference domain that has a simple shape and is diffeomorphically equivalent to all the Ω^θs. For instance, we choose a hollow semi-sphere as Ω⁰ as a simple shape visually close to the left ventricle in example 3. In general, one may select one particular ({varOmega }^{{theta }_{i}}), with θ_i ∈ Θ, as reference, or estimate a template shape, constrained to lie in {Ω^θ}, from a given dataset of sample domains using one of the many possible approaches developed for this purpose including, among others, refs. ^{30,31,32,33,34}. Although one can measure the similarity and distance between domains using a metric³⁵, that is, Chamfer distance^36,37, Earth Movers’ distance^38,39 or Riemannian metrics on shape spaces^21,40,41, this is not a prerequisite for successfully adopting this learning framework. This flexibility in choosing the reference domain facilitates a wide set of applications.

Estimating and encoding domain geometry with shape parameter

Once a reference domain Ω⁰ is chosen, the diffeomorphisms φ_θ that map Ω⁰ to the domains Ω^θ need to be constructed. In the case of a family of parameterized shapes, as in the examples of ‘Example 1 solving the Laplace equation’ below, the φ_θ can be constructed naturally by composing parameterizations, which also yields point correspondences, see ‘Domain generation’ in Methods.

For unparameterized data, however, such as the meshes in the example of ‘Example 2 learning reaction–diffusion dynamics’ and ‘Example 3 predicting electrical wave propagation’, point correspondences are not a priori available and the mesh structure itself may not even be consistent from one data sample to another. In such cases, the maps φ_θ are not known and need to be approximated for each domain. A variety of models can be used for this purpose relying, for example, on maps that are area-preserving⁴², quasi-conformal^43,44 or quasi-isometric⁴⁵, and which can be estimated, for instance, via the versatile functional maps framework of refs. ^19,46. Yet, in some applications, one may need a larger class of possible deformations, especially if larger distortions occur between different domains. For that reason, in the present work, we choose to rather rely on the diffeomorphic registration setting introduced in ref. ²¹, known as Large Deformation Diffeomorphic Metric Mapping (LDDMM). This model has several notable advantages when it comes to the applications we consider here. First, it generates transformations as flows of smooth vector fields that result in smooth diffeomorphisms of the whole ambient space ({{mathbb{R}}}^{d}), which is consistent with the theoretical setting developed in the previous section. From these estimated deformations, one can easily recover approximate point correspondences between Ω⁰ and the other domains, as well as map not only functions but also vector fields or tensor fields from one domain to another. Another interesting feature of LDDMM is the fact that it is connected to a Riemannian metric on the diffeomorphism group⁴⁷. Thus, any optimal deformation path in that model can be interpreted as a geodesic and, as such, be represented compactly via some initial ‘momentum’ field defined on Ω⁰. The Riemannian setting further enables the extension of many statistical techniques to the space of deformations, including methods such as principal component analysis (PCA) for dimensionality reduction, as we discuss next.

In the perspective of learning the solution operator over a family of diffeomorphic domains, we also seek a representation of the deformations φ_θ that can be effectively used as input for the operator learning neural network. The estimator of the map φ_θ generally leads to high-dimensional objects, either a large set of point correspondences between the mesh of Ω⁰ and Ω^θ or as a set of momentum vectors attached to vertices of Ω⁰ in the case of the LDDMM framework described above. To obtain an informative representation encoded by lower-dimensional shape parameter (tilde{theta }), we apply dimensionality reduction (herein PCA; see ‘Principal component analysis’ in Methods for additional details). A first approach is to apply standard PCA to the set of displacement vectors ({{x-{varphi }_{theta }(x)}}_{xin {rm{lndmrk}}({varOmega }^{0})}), where lndmrk(Ω⁰) is a fixed set of landmark points in Ω⁰. Alternatively, when deformations are estimated from the LDDMM model, we instead leverage the geodesic PCA method⁴⁸ on either the momentum or the deformation representation. In either case, projection onto the first p′ principal components leads to our estimated low-dimensional representation (tilde{theta }) of the shape parameter θ for each Ω^θ, and gives a more compact representation of φ_θ. Notice that we adopt only reduced-order PCA coefficients to represent the shape of Ω^θ for network training, but still rely on the originally (non-reduced) estimated mappings φ_θ to transport the estimated solution on Ω⁰ back to Ω^θ. It is also noteworthy that a low-dimensional representation of the mapping facilitates the network scalability as representing the diffeomorphism and geometry inefficiently can lead to a substantial expense of computational resources and lead to drastic reductions in performance. We compare an efficient and an inefficient approach to geometry encoding, or parameterization, in example 3 and Supplementary Section 3.

Example 1 solving the Laplace equation

In this section, we present the network prediction for the pedagogical example of the Laplace equation discussed above.

PDE problem

The PDE problem on a domain Ω^θ is

where for the boundary conditions we use the Gaussian random field (GRF) with the covariance kernel:

Data preparation

The process of data preparation is illustrated in Fig. 2a. Following the steps detailed in ‘Domain generation’ in Methods, we first generate 3,500 samples of the shape parameters θ and create the corresponding domains ({varOmega }^{{theta }_{i}}), which are deformations of the unit square, which itself is set as the reference domain Ω⁰. We then impose a boundary condition sampled from a GRF with a length scale l = 0.5 and solve the governing equation using a finite element solver. At the end of data preparation, we map the PDE solution from ({varOmega }^{{theta }_{i}}) to Ω⁰ for network training. The simulations are generated using FEniCS⁴⁹.

a, Data generation on N parametric two-dimensional domains. Landmark points are matched across two-dimensional domains with different meshing. Shape parameter (tilde{theta }in {{mathbb{R}}}^{{p}^{{prime} }}) is calculated by PCA on the deformation field at the landmark points. Here we adopt the first 15 principal components as (tilde{theta }). The PDE is solved using finite elements and mapped onto the reference domain. b, Neural operator structure. Shape parameter (tilde{theta }) and boundary condition (tilde{v}) are fed into the geometry (Geo.) and boundary condition (BC) branch, respectively. Coordinates in the reference domain x are the input of the trunk net. ⨂ represents pointwise multiplication. We adopt a fully connected neural network as the underlying structure in each branch. c, Network predictions (u_NN) and their absolute errors with numerical solutions (∣u_FEM − u_NN∣) on three testing domains. The color bars present the magnitude of solutions and prediction errors. d, Distributions of the mean absolute error ε_abs, and of the relative L₂ error (ε_L2) on the testing dataset with the corresponding means (vertical black lines). The testing dataset contains n = 197 cases. e, The average of ε_L2 (({bar{varepsilon }}_{{mathrm{L}}2})) with standard deviation for the training (red) and testing dataset (blue) is plotted against the number of training cases. Data are presented as mean ± s.d.

Source data

Full size image

Construction of φ
_θ and (tilde{theta })

We obtain a set of point correspondences between 11 × 11 uniformly distributed landmarks on Ω⁰ to their images in ({varOmega }^{{theta }_{i}}), using the map ({varphi }_{{theta }_{i}}), which is considered known in this example (see ‘Domain generation’ in Methods). We visualize the deformation via vector fields in the second column of Fig. 2a, where the length of the arrows corresponds to the magnitude of the deformation. Next, with the identified point correspondence and deformation field, each domain ({varOmega }^{{theta }_{i}}) can be parameterized using truncating principal component coefficients in PCA, yielding the low-dimensional shape parameter (tilde{theta }). Although the diffeomorphisms in this example are explicitly known, we intentionally use PCA to parameterize the shape to demonstrate the generalization of our framework when the diffeomorphisms are unknown. A comparison of network performance using θ and (tilde{theta }) can be found in Supplementary Section 4.

Network training and performance

Figure 2b illustrates the network architecture for approximating the latent operator on the reference domain for this example. As the new operator is a function of shape parameters and boundary conditions, the network has two branch networks for inputting the truncated shape parameter (tilde{theta }) and boundary values represented by a set of discrete points, denoted as (tilde{v}). The trunk network takes the coordinates x on the reference shape as input. We train the network on n = 3,303 training cases (see Supplementary Section 6 for details) and use the remaining n = 197 cases for testing. Network predictions in Ω⁰ are then mapped back to the original domain via φ_θ for further visualization and error analysis. Figure 2c shows network predictions u_NN and the absolute pointwise errors ∣u_FEM(x) − u_NN(x)∣ on three representative domains in the testing cases, indicating that network predictions are in good agreement with the numerical solutions. The maximum value of the absolute pointwise error is less than 0.02. We summarize the statistics of the mean absolute pointwise error ε_abs and relative L₂ error ε_L2 ≔ ∣∣u_FEM − u_NN∣∣₂/∣∣u_FEM∣∣₂ in the testing cases by presenting their distributions in Fig. 2d. Both distributions are left-skewed. The average ε_abs, denoted by ({overline{varepsilon }}_{{mathrm{abs}}}), and the mean relative L₂ error ({overline{varepsilon }}_{{mathrm{L2}}}) are 4.3 × 10⁻³ and 8.3 × 10⁻³, respectively. Overall, these distributions show that both measures of error are well distributed around and below their mean values, and only in a few extreme cases they are close to their maximum value. The behavior of train and test error as a function of the number of training cases is represented in Fig. 2e. ({bar{varepsilon }}_{{mathrm{L2}}}) of the testing dataset decreases to the same order of training error with an increasing number of training cases, from O(10⁰) to O(10²). On the basis of the above results, we conclude that our framework enables effective learning of the solution operator for the Laplace equation on a diffeomorphic family of domains.

Recall that, in the case of the Laplace equation considered here, we proved that sufficient conditions for Theorem 1 to hold included that the domains have ({{mathcal{C}}}^{2}) boundaries (see the discussion after Theorem 1, and in Supplementary Section 1). We have elected here to consider domains with corners, to demonstrate that at least in some cases our approach appears to be robust to some violations of such regularity assumptions sufficient, but perhaps not necessary, for Theorem 1. Note that in this case, the deformations ‘preserve’ corners, in a well-conditioned way, and do not create new corners, which may explain the good generalization power of our approach, notwithstanding the violation of regularity assumptions on the boundary of the domains.

Example 2 learning reaction–diffusion dynamics

In this section, we consider a PDE that includes time and is nonlinear.

PDE problem

We now consider a PDE that includes time and is nonlinear: a reaction–diffusion system in the form

where the Ω^θs are elongated elliptical domains with a central hole, and Ω⁰ is a circular annulus. The reaction term R(u) is adopted from the Newell–Whitehead–Segel model⁵⁰ to describe post-critical Rayleigh–Bénard convection. We impose a Neumann boundary condition and impose initial conditions by sampling from a GRF.

Data preparation

We visualize the data generation and learning process in Fig. 3a: we generate N = 6,000 sets of shape parameters θ following the steps in ‘Domain generation’ in Methods. Next, we simulate the system dynamics from t = 0 to t = 2 with a finite element method and map the numerical solution at different snapshots to the reference domain.

a, Data preparation on N parametric domains. Each domain is parameterized by either the deformation or the momentum field at the landmark points with p′ principal component coefficients. A finite element method is adopted to numerically solve the reaction–diffusion equation with various initial conditions (IC) on ({varOmega }^{{theta }_{i}}), set as an annulus, and map the solution to Ω⁰ at different time snapshots. b, Neural operator structure. Truncated shape parameter (tilde{theta }) and initial condition (tilde{v}) are fed into the geometry (Geo.) and initial condition (IC) branch, respectively. Coordinates in the reference domain x are the input of the trunk net. ⨂ represents pointwise multiplication. We adopt a fully connected neural network as the underlying structure in each branch. c, Network predictions with true shape parameters of the affine transformation at t = 0, 1 s and 2 s and their absolute errors on three testing domains. The color bars present the magnitude of solutions and prediction errors. d, Distributions of the relative L₂ error (ε_L2) obtained from four geometry parameterization approaches on the testing dataset with the corresponding means. The four approaches are affine with true shape parameters, LDDMM with PCA on momentum and deformation, and LDDMM with true shape parameters. The corresponding means (vertical black lines) are shown in the table. The number of testing cases is n = 297. Affine, affine polar transformation; Parameter, true shape parameter.

Source data

Full size image

Construction of φ
_θ and (tilde{theta })

To demonstrate the compatibility of our framework with generic methods of domain mapping, we adopt two approaches for estimating point correspondences between ({varOmega }^{{theta }_{i}}) and Ω⁰ (Fig. 3a): an affine polar transformation (referred to as ‘affine’ for the rest of this section) and LDDMM, with details provided in details in ‘Large deformation diffeomorphism metric mapping’ in Methods. The former approach converts the Cartesian coordinates of ({varOmega }^{{theta }_{i}}) into polar coordinates with the radius normalized to [0.5, 1.0]. These affine transformations are less general than LDDMM, as they are tailored to the particular shapes of Ω⁰ and ({varOmega }^{{theta }_{i}}). With the identified point correspondence, we proceed to calculate the truncated shape parameters (tilde{theta }) using PCA based on (1) deformation from LDDMM and (2) momentum from LDDMM.

Network training and performance

Network training in this work follows the steps presented in Supplementary Algorithm 1. Figure 3b shows the architecture of the network. The network contains a branch for encoding the truncated shape parameter (tilde{theta }) and one for the initial conditions f. x and t are the coordinates in Ω⁰ and time. We train a network with 5,703 training cases and examine its performance with 297 testing cases. Figure 3c shows the predicted solutions and the absolute errors for three representative testing cases at t = 0, 1 s and 2 s. (tilde{theta }) are adopted as the true shape parameters. Qualitatively, the network predictions closely match the finite element solutions with low absolute errors. Figure 3d illustrates the relative L₂ error distribution calculated over the 297 testing cases from various point correspondence algorithms, including (0) affine with true parameter and (1)–(3) LDDMM with PCA on momentum, true parameter and PCA on deformation, where the true parameters refer to the shape parameters in ‘Domain generation’ in Methods. All of the distributions show left skewness with means (black line) ranging from 3.2 × 10⁻² to 7.5 × 10⁻². Mean errors from affine transformation are smaller than those of LDDMM due to the more uniform distribution of landmarks in ({varOmega }^{{theta }_{i}}) and no matching error between Ω⁰ and ({varOmega }^{{theta }_{i}}). A comparison of affine transformation and LDDMM is presented in Supplementary Section 5. Nevertheless, the above results indicate that DIMON can accurately learn the reaction–diffusion dynamics on the diffeomorphic family of domains with a flexible choice of point-matching algorithms.

Example 3 predicting electrical wave propagation

In this section, we demonstrate the capabilities and scalability of our framework for predicting electrical signal propagation on the left ventricles (LVs) reconstructed from patient-specific imaging scans.

PDE problem

Human ventricular electrophysiology is described by the following mono-domain reaction–diffusion equation:

where C_m is the membrane capacitance, u is the transmembrane potential, D is a conductivity tensor controlled by the local fiber orientation, I_stim is the transmembrane current from external stimulation, and I_ion is the sum of all ionic current. I_ion is calculated based on a system of ordinary differential equations with more than 100 equations. Therefore, we refer readers to find a comprehensive description of I_stim, I_ion, model parameters and the underlying ordinary differential equations in refs. ^51,52. We add the cellular model downloaded from the CellML repository to our data repository. More details can be found in ‘Data availability’. It is important to note that the system is essentially anisotropic and multiscale.

Data preparation

Figure 4a provides an overview of training data generation. We collected 1,006 anonymized cardiac magnetic resonance (CMR) scans from patients at Johns Hopkins Hospital. However, our goal in this work is not to predict the full solution of this multiscale system at all times; we focus on two clinically relevant quantities, the distributions of activation times (ATs) and repolarization times (RTs) of a propagating electrical signal, defined as the time when local myocardium tissue is depolarized (activated) and repolarized. For each LV, we apply an external electrical stimulation (pacing) at seven myocardium points (Fig. 4b) in each segment and record the local ATs and RTs for each elicited wave (visualized in Fig. 4a) for network training and testing. We provide more details of data generation in ‘Cohort and simulations details in example 3’ in Methods.

a, Data preparation for the network training. The cohort assembled consists of 1,006 CMR scans of patients from Johns Hopkins Hospital, based on which LV meshes and fiber fields are generated. Next, we simulate a paced beat for 600 ms at an endocardial site until the LV is fully repolarized and record the ATs and the RTs for network training. b, Pacing locations (marked in white balls) located on the endocardium with reduced American Heart Association (AHA) LV segments from zones 0 to 6. c, Network structure. ⨂ represents pointwise multiplication. We adopt a fully connected neural network as the underlying structure in each branch. d, UVC calculation for registering points across geometries.

Full size image

Construction of φ
_θ and (tilde{theta })

We choose a hollow semi-sphere with an inner radius of 0.5 and an outer radius of 1 as Ω⁰ for LVs as they are diffeomorphically equivalent. To calculate point correspondence between these non-rigid and unparameterized LV meshes with Ω⁰, we adopt a registration method by matching the universal ventricular coordinates (UVCs)^53,54. As depicted in Fig. 4d, UVC converts Cartesian coordinates of the LV into 3 new coordinates in fixed ranges: apicobasal (ρ ∈ [0, 1]), rotational (ϕ ∈ [0, 2π]) and transmural (δ ∈ [0, 1]). Here, ρ and δ represent a normalized ‘distance’ to the basal and epicardial surfaces, while ϕ represents a rotational angle with respect to the right ventricle center. We calculate the UVCs for each LV in the cohort and establish their correspondence to Ω⁰ by matching their UVCs. Once the point correspondence is attained, we perform PCA on the coordinate difference at landmark points to derive (tilde{theta }), a low-dimensional representation of the shape parameter θ. Supplementary Section 3 presents network performance with LDDMM as the registration method.

Notably, we assume that the fiber field depends solely on the shape of the LV⁵³, thereby encoding the LV shape with (tilde{theta }) simultaneously leads to encoding the fiber field. To illustrate how the fiber fields influence electrical propagation, we present three exemplary cases with ATs on the reference domain in Supplementary Section 7, each with the same pacing location.

Network training and performance

We study the neural network performance in predicting ATs and RTs on patient-specific LVs. The network architecture is presented in Fig. 4b. We input shape parameters (tilde{theta }) along with pacing locations ({hat{x}}_{{mathrm{pace}}}) into two separate branches. The trunk network takes UVCs (x) of each training point as input. We present the network prediction in the top panel of Fig. 5. After random shuffling, we split the training dataset (n = 1,006) into 10 subsets with 100 geometries in sets 1–9 and 106 geometries in set 10. First, we train a network using the geometries and the ATs and RTs in sets 1–9 and set 10 for testing. We visualize predicted ATs and RTs along with their absolute errors for three representative LVs from the testing cohort. We observe that ATs and RTs on each LV with various pacing locations are faithfully predicted by our framework, with the maximum absolute error of ATs and RTs being around 20 ms (purple areas in the ‘Absolute error’ columns in Fig. 5). This error is relatively small compared with the maximum values of ATs and RTs.

Top: LV shape with their predicted ATs and RTs and absolute errors. The red stars are the pacing locations. The color bar is selected to be consistent with the CARTO clinical mapping system, with red denoting early activation and progressing to purple for late activation. The color bars present the magnitude of solutions and prediction errors. Bottom left: distributions of the relative L₂ error of ATs and RTs on the testing dataset with the corresponding means (vertical black lines). Pacing segment ID ranges from 0 to 6. Bottom right: bar plots of the mean relative L₂ errors with standard deviation from tenfold cross-validation. Data are presented as mean ± s.d.

Source data

Full size image

To quantitatively investigate how well the network predicts for the testing cases, we present the distribution of relative L₂ and absolute error in the bottom panel of Fig. 5. Each row represents a different myocardial segment as defined in Fig. 4b. The error distributions are roughly centered around their respective means (black lines) with left skewness. However, for apical regions (segment 6), both errors are slightly larger than for the other regions, which could be attributed to the complex fiber architecture created by rule-based methods at the apex⁵⁵. More specifically, we found that for the three cases with the largest error, the reconstructed LV shape unfaithfully reflects the true shape of the LV due to the collective artifacts from data acquisition and imaging segmentation. We discuss this further in Supplementary Section 8.

Furthermore, we perform 10-fold cross-validation to quantify the generalization ability of the network, for example, adopting sets 2–10 for training and set 1 for testing. The bottom-right panel shows the relative and absolute errors from 10-fold cross-validation along with their means (0.018 and 0.045) and standard deviations. In general, relative errors of ATs from ten iterations are larger than the RTs errors, although the magnitude of errors in ATs is smaller than the RTs.

Finally, we investigate the scalability and efficiency of DIMON. Figure 6 presents an estimation of memory usage when adopting an efficient and inefficient approach of geometry parameterization with different spatial resolutions in the training data. We can see that an inefficient parameterization approach (red regime), that is, voxelizing the LV and the ATs and RTs^17,56, represents the geometry in a higher dimension and leads to a sharp increase in memory usage with the increase of training samples. To incorporate pathophysiological features reflected in computed tomography (CT) and magnetic resonance imaging (MRI) images, one should train the network with data at MRI- and CT-level resolution. This can further exacerbate the need for computational resources, making the network training even more expensive. However, reducing the dimensionality with an efficient geometry parameterization approach (such as PCA) can alleviate this situation and make the training scalable even with higher resolutions. The black line represents an estimation of memory usage with more training data and the dot stands for the training cost in this case. In conclusion, our framework demonstrates that a neural operator can efficiently predict patient-specific electric propagation on realistic heart geometries with satisfactory accuracy, substantial speedup and scalability in computation. In addition, we tabulate the computational cost in Extended Table 1 between DIMON and openCARP, a traditional finite elements solver and used widely by the cardiac computational modeling community. Our neural operator substantially accelerates the overall speed in testing with a short training time: it requires only 9 min for training and less than 1 s on a single graphics processing unit to predict the ATs and RTs for a new patient, whereas it takes our solver in openCARP 3 h on 48 central processing unit nodes to simulate ATs and RTs in a single beat, not accounting for the additional time spent pre-processing and meshing.

Memory usage estimation given training data at the spatial resolution of CT (dashed) and MRI (dashed and dot) using inefficient (red regime) and efficient (blue regime) approaches of geometry parameterization. The black dot indicates the memory usage of DIMON. Memory usage for the inefficient approach is estimated based on data voxelization.

Full size image

We also perform a comparison between DIMON and Geometry-Aware Fourier Neural Operator (Geo-FNO)¹⁷, a representative attempt of learning operators on multiple geometries^15,16,17,56, for predicting ATs and RTs on LVs. The results demonstrate that DIMON has better efficiency, accuracy and scalability for learning on families of 3D complex shapes. Details regarding this comparison are presented in Supplementary Section 2.

This example demonstrates that our framework enables real-time human cardiac electrophysiology predictions. Model validation on such a large-scale realistic cohort is not only very rare given the huge efforts on data collection and high computational demands but also lends credibility to the model applicability and scalability in engineering applications given its high prediction accuracy. In addition, the learning ability of DIMON reaches beyond solution operators of PDEs. The ATs and RTs are the times when the PDE solution, transmembrane potential, exceeds or decreases below certain thresholds, and therefore functionals of solutions of the PDE, rather than solutions themselves.

Our framework provides an approach that enables fast prediction of PDE solutions on multiple domains and facilitates many downstream applications using artificial intelligence. One concrete example arises from cardiology. For instance, in cardiac electrophysiology, an approach to examine the arrhythmia inducibility of the substrate is to perform simulations based on the patient’s heart shape acquired from high-quality imaging scans. Although this is effective², the excessively high computational cost poses a substantial challenge to its vast application and implementation in clinics. With our framework, one can train a neural operator that predicts electrical propagation on various hearts without the need to perform expensive numerical simulations. Our framework is also promising for topology optimization, where shapes are optimized to meet certain design requirements, and PDEs need to be solved repeatedly on a large number of domains during such optimization procedure. DIMON allows for the computation of the derivative of the cost functional with respect to the parameters that describe the domain shapes⁵⁷ via automatic differentiation. This, in turn, simplifies the calculation of admissible deformations in shape optimization. This framework conveniently allows imposing boundary conditions, or initial conditions, or local material properties on different geometries.

DIMON also has several limitations. We consider only mapping scalar functions in this work, whereas mapping vector or tensor fields is yet to be addressed given that it holds particular importance in representing stress and velocity in fluid and solid mechanics. Incorporating methods that transport vector and tensor fields across shapes or manifolds^21,58,59 can potentially address this issue and will be of interest in the future. Also, although PCA is indeed a general approach for parameterizing shapes irrespective of their topology, other local methods for shape parameterization, such as non-uniform rational B-spline (NURBS), can be adopted due to their explicit form of splines or polynomials^60,61. In addition, conducting a rigorous analysis of the network’s convergence rate is beyond the scope of this study, making it difficult to estimate a priori how large of a training set is needed to achieve a given accuracy of the solutions. This framework is designed with the intention to learn operators on a family of diffeomorphic domains, and learning operators on non-diffeomorphic or topologically different domains is beyond the scope of DIMON. This is a challenging problem, not only because of the difficulty of modeling deformations combined with topological changes but also because PDE solutions tend to heavily depend on the topology of the domain.

Large deformation diffeomorphism metric mapping

We give a brief summary of the LDDMM framework that is used specifically to estimate diffeomorphic mappings between the domains of example 2, but that could more generally apply to a variety of different situations and geometric objects. The interested reader can further refer to refs. ^21,47 for additional details on the model.

The central principle of LDDMM is to introduce diffeomorphic transformations of ({{mathbb{R}}}^{d}) which are obtained as the flows of time-dependent vector fields. More precisely, given a time-dependent integrable vector field (tin [0,1]mapsto v(t,* )in {C}_{0}^{1}({{mathbb{R}}}^{d},{{mathbb{R}}}^{d})) (the space of C¹ vector fields on ({{mathbb{R}}}^{d}) that vanish at infinity as well as their first derivatives). Then the flow map φ^v of v, defined by ({varphi }^{v}(t,x)=x+mathop{int}nolimits_{0}^{t}v(s,{varphi }^{v}(s,x)){mathrm{d}}s), can be shown to be a C¹ diffeomorphism of ({{mathbb{R}}}^{d}), where s is a standard notation for a dummy variable. The group of all such flows taken at the terminal time t = 1 can be further equipped with a metric as follows. One first restricts to a given Hilbert space V of vector fields in ({C}_{0}^{1}({{mathbb{R}}}^{d},{{mathbb{R}}}^{d})) (for example a Sobolev space of sufficient regularity or reproducing kernel Hilbert space with adequate kernel function) and define the energy of the flow map φ^v(1, ⋅ ) by (mathop{int}nolimits_{0}^{1}parallel v(t,* ){parallel }_{V}^{2}{mathrm{d}}t). This provides a quantitative measure of deformation cost and, given two shapes Ω and Ω′ in ({{mathbb{R}}}^{d}), an optimal transformation mapping Ω to Ω′ can be found by introducing the registration problem:

In practice, it is common to further relax the boundary constraint ({varphi }^{v}(varOmega )={varOmega }^{{prime} }) based on a similarity measure between the deformed domain φ^v(Ω) and Ω′. This is typically done to ensure the robustness of the method to noise and inconsistencies between the two shapes.

Optimality conditions for the above problem can be derived from the Prontryagin maximum principle of optimal control (compare Ch. 10 in ref. ⁴⁷) from which it can be shown that a minimizing vector field for equation (6) can be parameterized by an initial costate (or momentum) variable. Furthermore, when Ω is a discrete shape (that is represented by a finite set of vertices), this initial momentum can be identified with a distribution of vectors over the vertices of Ω. This allows us to reduce the registration problem to a minimization over the finite-dimensional initial momentum variable, which can be tackled for instance with a shooting approach. For the applications presented in this paper, we make use specifically of the implementation of diffeomorphic registration from the MATLAB library FshapesTk.

Principal component analysis

Consider p landmark points on Ω⁰ with known point correspondences on each ({varOmega }^{{theta }_{i}}) given N domains, (Ain {{mathbb{R}}}^{ptimes N}) denotes the Euclidean difference between the target domains and the reference domain in each direction. We define (bar{A}=A-mu), where (bar{A}) is normalized to zero mean. We perform the singular value decomposition (bar{A}=U,Sigma {V}^{T}), where (bar{A}in {{mathbb{R}}}^{Ntimes p}), (Uin {{mathbb{R}}}^{Ntimes p}), (varSigma in {{mathbb{R}}}^{ptimes p}), ({V}^{T}in {{mathbb{R}}}^{ptimes p}) and T is the standard notation for matrix transpose. We truncate U and Σ to first p′ rank and obtain the reduced matrices as ({U}_{{mathrm{r}}}in {{mathbb{R}}}^{Ntimes {p}^{{prime} }}), ({varSigma }_{{mathrm{r}}}in {{mathbb{R}}}^{{p}^{{prime} }times {p}^{{prime} }}) and ({V}_{{mathrm{r}}}^{T}in {{mathbb{R}}}^{{p}^{{prime} }times {p}^{{prime} }}). We define the coefficient matrix D = U_rΣ_r, where each row in (Din {{mathbb{R}}}^{Ntimes {p}^{{prime} }}) is a reduced representation of the deformation from Ω^θ to Ω⁰, referred to as reduced shape parameter (tilde{theta }).

Domain generation

We generate the computational domain in example 1 following the equations below.

where X, Y ∈ [0, 1] × [0, 1] are the coordinates in the reference domain, and x and y are their corresponding coordinates on newly generated shape. a_i and b_j are shape parameters, all chosen independently as follows: a₁, a₃ and b₁, b₃ from the uniform distribution in [−0.5, 0.5] and a₂, b₂ from the uniform distribution on [0, 0.75].

In example 2, we define the reference domain as an annulus with inner and outer radii at 0.5 and 1.0, respectively. The parametric family of domains is rotated ellipsis with a void. We sample the shape parameters following:

Here, c₁ and c₂ stand for the length of the semi-major and minor axes, c₃ is the rotational angle, and c₄ is the radius of the inner circle.

Neural operator

In this section, we briefly summarize the architecture of MIONet¹⁸. Notice that our framework is inclusive of the architecture of the neural operator we use to approximate ({{mathcal{F}}}_{0}). We denote ({tilde{{mathcal{F}}}}_{0}) as an approximation of the mapping from the m + 1 input functions [θ, v₁, …, v_m] to the output function u. We remove the subscript that denotes the domain for clarity. We then define m + 1 branch networks that input a discrete representation of each function and a trunk network that takes coordinates x ∈ Ω⁰ as input. Finally, the output function value at point x is approximated by

where ({tilde{{bf{g}}}}_{i}) (called branch net i) and (tilde{{bf{f}}}) (called trunk net) are neural networks, ⊙ is the Hadamard product, and ({mathcal{S}}) is the summation of all the components of a vector¹⁸. q₀, q₁…, q_m are positive integers. Equation (8) can be written in a simplified form as:

({b}_{i}^{{mathrm{geo}}}) is the output of the Geo. branch given θ, t_i is the trunk network at ith neuron, and ({b}_{j}^{i}) is the output of ith neuron from jth branch network^9,18. In this work, we adopt the mean squared error as the loss function.

Cohort and simulations details in example 3

This cohort includes patients with hypertrophic cardiomyopathy (HCM) who were treated at the HCM Center of Excellence at the Johns Hopkins Hospital from 2005 to 2021. This study complies with all relevant ethical regulations and was approved by the Johns Hopkins Medicine institutional review boards (approval number IRB00205270). Our dataset consists of de-identified late gadolinium-enhanced CMR (LGE-CMR) scans from over 850 patients. The LGE-CMR scans have slice thicknesses ranging from 6 mm to 10 mm and spatial resolutions varying from 1.17 mm to 2.56 mm. Notice that some patients have multiple scans over time, which sums up to 1,006 scans.

To simulate electrical propagation, we first segment the myocardium and the blood pool from the raw images. We then reconstruct a mesh and generate fibers for each LV based on the segmented images. The average length of mesh size is 400 μm, leading to an average number of vertices on the order of 4 million^2,62. To account for the directionality of the electrical signal propagated along the fibers, we adopt the validated rule-based method proposed in ref. ⁵³ to generate the myocardial fibers in each patient’s LV.

Next, we divide the myocardium surface into seven segments, which is a simplified version of the standardized myocardium segmentation from the American Heart Association^63,64. Within each segment highlighted with a different color in Fig. 4, we simulate a paced beat for 600 ms at a randomly picked endocardial site until the LV is fully repolarized. Specifically, ATs and RTs are chosen as the time when the transmembrane potential u reaches 0 mV from the resting state (−85 mV) and the time when u decreases below −70 mV, recovering from depolarization. More details regarding the solver and simulation procedure can be found in refs. ^2,65.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.