Abstract
In social science, formal and quantitative models, ranging from ones that describe economic growth to collective action, are used to formulate mechanistic explanations of the observed phenomena, provide predictions, and uncover new research questions. Here, we demonstrate the use of a machine learning system to aid the discovery of symbolic models that capture non-linear and dynamical relationships in social science datasets. By extending neuro-symbolic methods to find compact functions and differential equations in noisy and longitudinal data, we show that our system can be used to discover interpretable models from real-world data in economics and sociology. Augmenting existing workflows with symbolic regression can help uncover novel relationships and explore counterfactual models during the scientific process. We propose that this AI-assisted framework can bridge parametric and non-parametric models commonly employed in social science research by systematically exploring the space of non-linear models and enabling fine-grained control over expressivity and interpretability.
Introduction
Quantitative and formal models are widely employed in economics, sociology, and political science (Gailmard and Patty, 2012; Oliver, 1993) for studying diverse subjects ranging from economic growth (Solow, 1956) to participation in social movements (Granovetter, 1978). They are also used to describe empirical regularities, such as patterns in voting behavior and city scaling laws, from which explanatory mechanisms can be derived and subsequently tested (Chatterjee et al. 2013; Gabaix, 1999). While qualitative methods remain the dominant paradigm in much of social science due to their ability to capture greater nuance and extrapolate from sparse data, mathematical models can complement our understanding of social phenomena. They help us reason about underlying mechanisms, generate new research questions, and produce empirically testable predictions (Epstein, 2008).
New quantitative models are typically constructed using a combination of existing theory, intuition about the relevant variables, and insights into how the variables interact. Researchers can often incorporate valuable ideas about social phenomena in this modeling process, making intuition a valuable priority. However, relying on human ideation alone suffers from two drawbacks. First, because the data can be high-dimensional, noisy, or strongly non-linear, it may be difficult to recognize certain empirical regularities. Second, social phenomena are often explained by a large space of plausible and intuitive theories (Keohane et al. 2021). This fact, in combination with hidden assumptions made during the modeling process, makes it difficult to search through the space of possible theories by hand. A common way these problems materialize is that the inclusion or omission of certain variables can change the sign of the estimated parameters. These issues can threaten the external validity of some models, especially if they are tested in isolation without a systematic examination of the entire solution space (Healy, 2017).
Machine learning provides a collection of powerful tools for detecting patterns in data. Our goal in this paper is to demonstrate that it can effectively complement social scientists in the theory-building process by introducing a framework that fosters a collaborative, iterative approach. The traditional challenge with machine learning methods is that they are often uninterpretable and cannot be generalized beyond the observed data. Furthermore, it is difficult to merge these techniques with human intuition, particularly in formalizing rigorous hypotheses about underlying social processes. Our approach pushes beyond existing methods by focusing on symbolic regression techniques that yield interpretable models, facilitating the development of robust, testable theories.
Symbolic regression—a method for discovering symbolic expressions from empirical data—has emerged as a central method for uncovering hidden relationships in complex data. It offers an exciting first step in incorporating scalable, data-driven methods in the model discovery process. Most symbolic regression methods employ genetic algorithms, which perform a targeted search over populations of candidate solutions using strategies inspired by biological evolution (Keren et al. 2023; Schmidt and Lipson, 2009). Other successful approaches include sparse regression (Brunton et al. 2016), Bayesian learning (Guimerà et al. 2020), deep learning (Biggio et al. 2021; Holt et al. 2023; Kamienny et al. 2022; Petersen et al. 2021), or a combination of these methods (Costa et al. 2021; Kubalik et al. 2023; Udrescu and Tegmark, 2020). In recent years, they have seen substantive use in the discovery of fundamental laws in the natural sciences including mathematical conjectures (Keohane et al. 2021), physical laws (Cranmer et al. 2020; Udrescu and Tegmark, 2020; Wang et al. 2019), and ecological models (Cardoso et al. 2020; Martin et al. 2018).
There have also been various applications of symbolic regression to social science data, including the exploration of factor importance in carbon emissions (Pan et al. 2019) and unemployment rates (Truscott and Korns, 2014), modeling of oil production (Yang et al. 2015), inference of strategic rules in repeated games (Duffy and Engle-Warnick, 2002), financial modeling (Liu et al. 2023), and in cognitive psychology (Liu et al. 2024). Furthermore, techniques for fitting non-linear dynamical systems models to data have been developed for studying complex phenomena such as school segregation (Spaiser et al. 2018) or the relationship between democracy and economic growth (Ranganathan et al. 2014, 2015).
Despite these advancements, two critical gaps persist in the current application of symbolic regression in social science research. First, most existing symbolic regression methods lack flexibility in incorporating user-specified inductive priors: a crucial element for seamless human-machine collaboration, particularly in cases where inference from sparse data can benefit greatly from human input. Without this flexibility, researchers are often confined to models that either rely heavily on predefined structures or those that lack theoretical grounding, which can limit the usefulness of machine-generated insights for hypothesis testing and theory-building. Second, existing symbolic regression methods are not well suited to handling longitudinal (panel) datasets, a common feature of social science data where time-series or cross-sectional data across different groups (e.g., countries, regions, or individuals) provide rich opportunities for understanding dynamic processes. Traditional methods fail to leverage the statistical power gained by pooling information across such datasets, limiting the generalizability and robustness of discovered models.
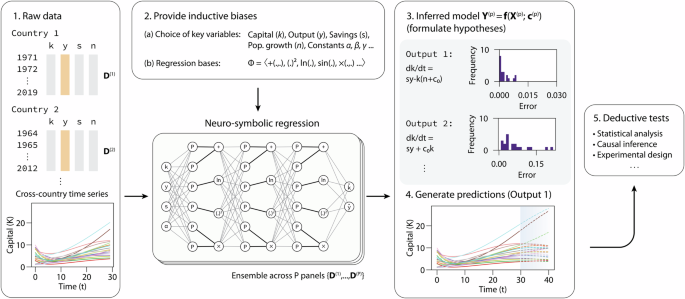
We address these problems in our work and propose a general framework for using neuro-symbolic regression to assist the discovery of quantitative models in social science. Building off OccamNet (Costa et al. 2021), a neural-evolutionary method for efficient symbolic regression, our system searches for parsimonious functional relationships or differential equations and evaluates them according to their explanatory power. We select OccamNet for the symbolic regression backbone as it combines the advantages of genetic algorithms and deep learning-based methods and specializes in fitting unordered and small datasets, which are prevalent in the social sciences. Furthermore, unlike other neuro-symbolic regression methods, OccamNet is fast and scalable as it is able to seamlessly search expressions in parallel using modern AI accelerators, such as GPUs and TPUs, and to enable weight-sharing for regressing on several models at once. We thus leverage OccamNet to extend existing symbolic regression methods on two fronts: (i) improving noise tolerance in small datasets and (ii) enabling the system to learn symbolic relationships across longitudinal data (e.g., in a panel dataset across countries) using a weight-sharing approach. This allows one neural-symbolic model to be trained on multiple panels with different parameters simultaneously. Using the proposed workflow shown in Fig. 1, these contributions allow neuro-symbolic methods to be more readily applied to ab initio model discovery in social science, where small and noisy datasets are often available across contexts with different model parameters.

Analogous to the inductive-deductive reasoning process, a dataset of interest (1)—which may be time-series, cross-sectional, or longitudinal—is supplied to OccamNet. The user can provide inductive priors (2), such as the choice of key variables, known constants, or specific functional forms to constrain the search space. OccamNet finds interpretable and compact solutions that model the input data by sampling functions from an internal probability distribution represented using P-nodes (Costa et al. 2021). In this example, OccamNet recovers the governing equation of the Solow-Swan model of economic growth (Solow, 1956) from a synthetic dataset. Each formal model is characterized by its error distribution in the training set (3), allowing the user to identify outliers and interrogate its internal validity. The symbolic model is then used to generate predictions (4) to perform deductive tests across unseen data, either by partitioning a test set or informing experimental designs (5).
We highlight several key applications of this system in a social science context. First, we show that complexity regularization can be used to find higher-order corrections in network degree distributions, which we extend in mapping the complexity-accuracy Pareto front of economic production functions. We argue that such maps can help researchers find a trade-off among various quantitative models and debias the search process. Next, we apply this method to dynamical models, where we use real-world, noisy data to discover the Lotka-Volterra equations and show that weight-sharing learning can be applied across epidemic waves to provide better performance in finding compartmental models. Finally, we highlight the utility of neuro-symbolic regression in evaluating existing models by using weight-sharing learning to map the complexity-accuracy front of economic growth models across 18 OECD countries and evaluate the generalizability of Solow and Swan’s exogenous growth model (Solow, 1956; Swan, 1956). We hope that the capabilities demonstrated in this article will inspire greater collaborative use of these machine-learning methods in social science.
Method
Figure 1 outlines our workflow for AI-assisted model discovery in social science. Symbolic regression allows us to uncover interpretable expressions as opposed to black-box or fully non-parametric results. These expressions, which may take the form of differential equations, scaling laws, or functional relationships, can shed light on the interactions between variables and help social scientists generalize beyond linear relationships. Furthermore, because symbolic laws can have system-specific constants, the inferred models also describe precise structural relationships that can be used to generate testable predictions across populations or timeframes. We employ a neural network architecture built on OccamNet to find sparse, interpretable formal models that fit the desired input data. In particular, we leverage OccamNet’s architecture to implement two key features to systematically explore the space of candidate models in social science: complexity regularization and data ensemble learning.
In the most general formulation, OccamNet takes as input a panel dataset of the form ({{mathcal{D}}}={{{{bf{D}}}}^{(1)},ldots ,{{{bf{D}}}}^{(P)}}) on K variables, where each dataset ({{{bf{D}}}}^{(p)}in {{mathbb{R}}}^{{N}_{p}times K}) with Np samples is partitioned by the user into an input set
and a target set
for symbolic regression, i.e., ({{{bf{D}}}}^{(p)}=left[{{{bf{X}}}}^{(p)}| {{{bf{Y}}}}^{(p)}right]). When the data is not longitudinal, we simply have p = 1 with one dataset ({{bf{D}}}=left[{{bf{X}}}| {{bf{Y}}}right]).
Alternatively, the user can also allow OccamNet to automatically find a partition by having it search through all possible combinations of inputs and targets and fitting an implicit function to the dataset(s). This mode of operation is useful if the user is seeking new empirical regularities in data and wishes to obtain a ranked list of candidate relations based on their error and compactness.
The goal of the regression problem is to find vectors of functions and hidden constant parameters ({{{bf{f}}}}^{(p)}=[{f}_{1}(cdot ,;{{{bf{c}}}}^{(p)}),ldots ,{f}_{{K}_{y}}(cdot ,;{{{bf{c}}}}^{(p)})]) that approximate or exactly specify each target variable ({y}_{i}^{(p)}={f}_{i}^{(p)}left({{{bf{x}}}}^{(p)}right)) with input vector ({{{bf{x}}}}^{(p)}in {{mathbb{R}}}^{{K}_{x}}) based on a predefined set of B basis functions ({{mathbf{Phi }}}={left{{phi }_{i}(cdot )right}}_{i = 1}^{B}) and maximum expression depth dFootnote 1. These basis functions can have any number of arguments, be specified over different domains, or include constants to be optimized over (e.g., power laws of the form xc). They may include pre-determined variables, such as π, e, the measured rate of capital growth, or the basic reproduction number of a virus. Furthermore, OccamNet can operate with piecewise functions or non-differentiable, potentially recursive programs like MIN(x0, x1, x2…), enabling a wide range of possibilities for constructing formal models.
OccamNet works by representing a probability distribution over a space of user-specified functions. During training, OccamNet samples S functions from its probability distribution, evaluates their effectiveness at fitting the given data, and updates its probability distribution so as to weight its probability toward better-fitting solutions. An overview of the implementation of OccamNet and its advantages over other neuro-symbolic regression methods for social science data is provided in Appendix A.
Regularization
Complexity regularization enables model discovery to follow the maxim that “the theory should be just as complicated as all our evidence suggests” (Keohane et al. 2021). This requirement does not necessarily depend on the assumption of parsimony: although it may be true that simpler theories are more probable (Zellner, 1984), it also helps to ensure, independently, that there is sufficient evidence in relation to the complexity of the model to yield clear and specific research designs. Furthermore, in the computational context, the function relating variables of interest often only consists of a few terms. This allows us to frame symbolic regression as a sparse regression problem, making model discovery computationally tractable and avoiding the need to perform a brute-force search over functions (Brunton et al. 2016).
To bias OccamNet toward simpler solutions, we include two regularization terms in the optimization objective, which the user can tune to control the simplicity of OccamNet’s output: Activation Regularization and Constant Regularization. These terms penalize the number of activation bases and the number of tune-able constants used in the resulting expression, respectively.
We further constrain the search space by exploiting dimensional analysis: a powerful technique in physics that is used to transform a problem into a simpler one with fewer variables that are all dimensionless. For instance, a dataset on economic growth might include variables with units such as dollars per capita or units of labor per year. Upon user specification of the units of each input and target variable, OccamNet checks whether the units of a sampled function match those of the target variable. It then adds a Unit Regularization term to penalize functions where the units do not match. While OccamNet may also add a unit-normalizing constant in front of the mismatched terms, this would come at the cost of additional complexity. The implementation of all of the regularization terms is described in more detail in Appendix A 1.
Data ensemble learning by weight-sharing
Unlike other symbolic regression contexts, social science data often contain both cross-sectional and time-series information. Take, for example, panel data containing economic indicators across several countries. Each country has a set of hidden constant parameters inaccessible to the researcher. Even if the variables of interest are related by the same functions, solutions to the dynamical system may be qualitatively very different because each country has different parameters and initial conditions. Learning on ensembles of data by sharing the neural network weights of OccamNet on multiple panels allows us to aggregate the statistical power of such datasets and reconstruct the dynamical equations even if there are hidden parameters, and if individual country trajectories do not traverse the full phase space of the system.
Consider a panel dataset across P panels, {X(1), …, X(P)} where the rows of each panel are time-dependent vectors of variables x(p)(t). Additionally, let each panel have a vector of hidden parameters ({{{bf{c}}}}^{(p)}={[{alpha }^{(p)},{beta }^{(p)},ldots ]}^{top }) that is inaccessible to the researcher. OccamNet is able to learn on ensembles of data by fixing a shared set of functions f(⋅) for all panels and fitting the optimal constants c(p) for each panel individually. The system repeats this step for a specified number of epochs and selects the optimal functions f*(⋅) with the lowest mean-squared error with respect to the target data. To support ensembles with datasets of varying sizes, we normalize the total error by dividing each individual dataset error by the number of samples in the given panel.
Since the loss computed at each epoch is a distribution across the panels, different summary statistics may be used to select the optimal symbolic model. For instance, the loss may be computed as the mean or median. However, because the model f(x) is generally non-linear, errors of the form f(x + ϵ), where ϵ is a vector of Gaussian distributed entries with zero mean, can lead to highly skewed distributions that require alternate measures of central tendency. It may also be the case that certain outliers require additional variables or theoretical models to explain. In this case, the researcher can choose to identify the optimal formal model from the error histogram. The data ensemble learning modality is demonstrated in Fig. 1.
Differential equation discovery
For time-dependent datasets, we wish to discover dynamical systems of the form (dot{{{bf{x}}}}(t)={{bf{f}}}({{bf{x}}}(t))), where x(t) is a vector denoting the state of the system at time t. The input to OccamNet is a time-series dataset
where we have N samples that are timestep h apart starting from an initial state at t0. Our regression target is then given by ({{bf{Y}}}=dot{{{bf{X}}}}).
Fitting dynamical equations follows the same procedure with the exception that Y is first computed numerically from the input data using the central difference formulaFootnote 2. Since each x(t) is often contaminated with noise, it may be necessary to filter both X and (dot{{{bf{X}}}}) to counter differentiation error, as described in Appendix A 2.
While we primarily evaluate OccamNet on systems of non-linear differential equations in which the target variables are decoupled, we note that our model can also be applied to coupled systems by fitting the equations individually and adding the output of each fit as an input variable. For instance, for a system of two ODEs (frac{d{x}_{1}}{dt}={f}_{1}({x}_{1},{x}_{2})) and (frac{d{x}_{2}}{dt}={f}_{2}({x}_{1},{x}_{2},frac{d{x}_{1}}{dt})) as regression targets, one can use OccamNet to fit (frac{d{x}_{1}}{dt}) and append the predicted time-series to the input data for fitting (frac{d{x}_{2}}{dt}).
Method scalability
Let S be the number of sampled functions at each layer, N be the total number of points in the input dataset, Kx and Ky be the number of input and target variables in the dataset, B be the maximum number of activation functions per layer, and D be the maximum expression depth. Then the total computational complexity of an OccamNet network with the ability to express BD possible expressions is bounded as
The full derivation is provided in Appendix A 3. This bound implies that holding all other parameters fixed, the complexity scales linearly in the number of functions sampled as well as in the size of the dataset, allowing our method to be used for large social science tasks. While the complexity scales quadratically in the number of basis functions per layer and in the depth, a crucial advantage of OccamNet is that it represents complete expressions with a single forward pass, thereby enabling sizeable gains in speed when using GPUs. A more detailed analysis of OccamNet’s scalability is provided in (Costa et al. 2021).
Case studies
We validate our AI-assisted approach on synthetic and real-world datasets covering both static distributions and dynamical equations that appear in social science applications. All dataset pre-processing details and model parameters are available in Appendix B.
Static distributions
We first evaluate our neuro-symbolic regression method for the discovery of social science models on static distributions without time dependence. We extract symbolic relations as illustrated in Fig. 2, which summarizes our results on fitting datasets of single variables such as network densification and degree distributions, as well as a multi-variable distribution for the Cobb-Douglas production function (Cobb and Douglas, 1928).
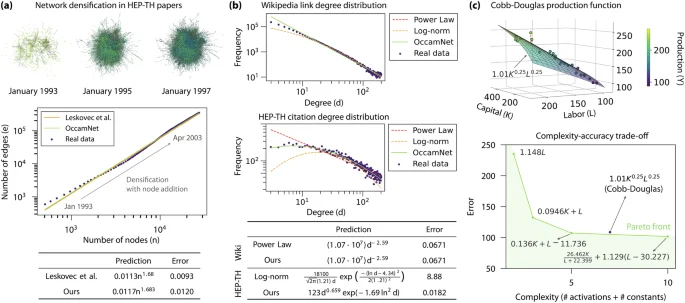
a Discovering the network densification process in paper citations. The top diagrams show the evolution of the arXiv high energy physics citation network over time. OccamNet is able to discover the correct functional form for the densification law axβ based on a table of network properties (Leskovec and Krevl, 2014). b A similar experiment is performed to discover the scaling law in the rank-size distribution of node degrees in the arXiv citation and Wikipedia hyperlink networks. At the same level of complexity regularization, OccamNet picks the simplest solution for each dataset, demonstrating the principle of Occam’s razor. Our model finds a power law for the Wikipedia network and a more complex function for the citation network. c We apply OccamNet to real-world, multi-dimensional economic data from Cobb and Douglas’s 1928 paper. The complexity-accuracy trade-off is evaluated by sweeping across the available modes of regularization.
Network properties
Beginning with Barabási and Albert’s seminal paper on scale-free networks (Barabási and Albert, 1999), graph formation properties and degree distributions have become an increasingly active area of research. Network structures are studied in economics and sociology in the context of clustering, information spread, and skewed distributions, such as those exemplifying the “rich get richer” effect in preferential attachment processes. Here, we focus on two sets of persistent properties observed in human networks: densification laws and degree distributions.
In Fig. 2a, we use neuro-symbolic regression to find the network densification process in citation networks. Densification occurs when the number of edges in a graph grows super-linearly in the number of nodes over time. We use OccamNet to reconstruct the densification law of the citation graph of high energy physics preprints on arXiv from January 1993 to April 2003, where the number of edges grows according to e(t) ∝ n(t)a as shown by Leskovec et al. (2005). Our fit closely matches their baseline with a densification law exponent of ~1.692, indicating that the number of citations in each paper, on average, grows over time. Note that we expect OccamNet to produce a fit with slightly higher error compared to the Ordinary Least Squares solution since our model has the additional task of finding the correct functional form before fitting the constants using gradient descent. For more accurate constant parameters, one may opt to take the functional form outputted by OccamNet and then fit the parameters using non-linear least squares.
Next, we use OccamNet to discover the functional form of various network degree distributions. Power-law distributions of the form k−α have been found in contexts ranging from hyperlink graphs (Albert et al. 1999) to biological networks (Albert, 2005). These distributions have been proposed to be universal across a wide range of systems, spawning extensive literature about their formation mechanisms and their links to network dynamics. However, alternative degree distributions like log-normal, Weibull, and exponential have also been observed in real-world networks, stimulating new work on finding alternative mechanisms that explain these functional forms (Broido and Clauset, 2019). Employing neuro-symbolic regression, we can go beyond the standard set of distributions to find any function drawn from the specified bases.
Figure 2b shows the degree distribution for both Wikipedia article links (Various, 2009) and the high energy physics citation network. OccamNet is trained on both datasets using the same complexity regularization. In the Wikipedia dataset, the system discovers the power-law distribution independently, while in the citation dataset, it finds that the degree distribution is better fit by a function of the form ({k}^{alpha }{e}^{-c{ln }^{2}(k)}). The two examples underscore the principle of Occam’s razor. For a given level of complexity regularization, the system picks the simpler functional form for the Wikipedia dataset because this dataset more closely resembles a power law. On the other hand, OccamNet discovers a more complex, but far more accurate expression for the HEP-TH dataset because this dataset deviates significantly from simpler models. The citation network fit performs better than both the power-law and log-normal distributions.
It is worth noting that using mean-square error minimization does not generally provide the optimal estimator for any particular degree distribution. For instance, least-squares fitting can produce inaccurate estimates for power-law distributions, and goodness-of-fit tests such as likelihood ratios and the Kolmogorov-Smirnov statistic must be used to evaluate the model (Clauset et al. 2009). However, in the case where the functional form is not known a priori, we opt to use mean-square error minimization as a Bayesian posterior with a non-informative prior. Other informative priors can be used when the set of functions is narrowed down, for instance, by performing maximum-likelihood estimation for each of the hypotheses proposed by the symbolic regression system.
Production functions
One of the best-known symbolic relations in economics is the Cobb-Douglas production function (Cobb and Douglas, 1928). Its introduction in 1928 represented the first time an aggregate production function was developed and statistically estimated (Biddle, 2012). Predicting that a stable relationship between inputs and outputs could be derived from empirical data, the authors found a robust linear relationship between the log output-to-capital ratio and the log labor-to-capital ratio of the American manufacturing industry. This relationship was later shown to hold across countries and timeframes (Douglas, 1976). The function has since been widely adopted as a measure of productivity, as a utility function, and as a foundation of subsequent models such as the Solow-Swan model of long-run economic growth (Solow, 1956; Swan, 1956).
In its most common form, the law states that the total production (output) Y of a single good with two input factors, capital K and labor L, is given by
where A is typically a constant representing total factor productivity (ratio of output not explained by the number of inputs), and α and β are the output elasticities of capital and labor, respectively. In cases where we expect to see constant returns to scale (i.e., an increase in the input quantity leads to an equivalent increase in the output), α and β are additionally assumed to satisfy the constraint α + β = 1.
Cobb and Douglas used a US manufacturing dataset covering annual production from 1899–1922 to fit the linear regression (log (frac{Y}{K})=A+beta log (frac{L}{K})) by ordinary least squares. The resulting constant parameters were given by A = 1.01 and β = 0.75, resulting in the equation Y = 1.01K0.25L0.75 which is plotted in Fig. 2c. We explore the expressions for Y predicted by OccamNet for the same dataset at varying levels of complexity regularization. We define the complexity value of an expression as the sum of the number of activation bases and constants. While there are other possible measures of complexity, such as the number of bits needed to store the symbol string of the expression (Udrescu and Tegmark, 2020), our definition matches the regularization options provided for OccamNet training as described in the Method section. We also note that any complexity metric will not be an exact measure of parsimony, which is typically defined according to the paradigmatic context through which the expression is interpreted.
The Pareto front of the complexity-accuracy trade-off from sweeping across Activation Regularization parameter values is shown in Fig. 2c. The full specification of model parameters is included in Appendix B 3. Without any regularization, OccamNet discovers an expression with lower loss and higher complexity than the Cobb-Douglas baseline. Moreover, with a small amount of regularization, our model finds an equation with both lower loss and lower complexity than the baseline. The Cobb-Douglas function, therefore, lies outside the Pareto front—under our particular definition of complexity—for the given US manufacturing dataset. We recover a Cobb-Douglas-like expression of the form K0.249L0.754 only after restricting the set of possible bases for the regression to the ones found in (5). With only 24 available samples available in the data, our model benefits from a stronger inductive prior on the target function to reduce the risk of over-fitting. While there are strong theoretical reasons to prefer the Cobb-Douglas function, OccamNet offers a method for both discovering new models and validating the existing expression.
This experiment reveals an important component of using AI-assisted model discovery in social science research. As discussed, the true definition of parsimony depends on how the expression is interpreted through an economic lens and not the length of the mathematical equation. How “good” a model is depends on how it is used: in some contexts, a good theory is simple and explains the majority of the observations, while in others, it is highly complex and resolves all the empirical phenomena.
Therefore, the use of symbolic regression must be viewed as a collaborative human-machine process. We can analogize model search as an optimization process across three dimensions: (i) the amount of variance explained by the model, (ii) its complexity, as per Occam’s Razor, and (iii) the meaning behind the terms and structure of the model, as interpreted in the context of the field. While we cannot algorithmically search (iii), our method provides a way to fix a point along that dimension via a choice of inductive priors and execute a systematic search along the first two dimensions. Furthermore, restricting the search space by injecting existing knowledge about the model (performed by customizing the library of bases) can be beneficial to the regression tasks, particularly on sparse and noisy datasets. The key insight is that while humans are still needed to interpret the resulting models, computational methods offer a powerful way to systematize our search through two key dimensions in the hypothesis space.
Dynamical laws
We next apply our neuro-symbolic regression method to differential equation discovery. OccamNet is primarily evaluated on systems of non-linear differential equations, where each ODE is fit independently. We use both synthetic and real-world datasets to fit models of predator-prey relationships, epidemiology, and economic growth.
Predator–prey relationships
Models of the relationships between predators and prey have wide-reaching implications beyond ecology, where they are used to describe the dynamics in biological systems. While these models—often taking the form of differential equations—were historically derived from first principles and rigorous theory-building, symbolic regression offers a promising tool for reverse-engineering them from data (Martin et al. 2018).
A simple yet paramount model of predator-prey interactions between two species is given by the Lotka-Volterra equations (Lotka, 1910),
where H and L are the populations of the prey and predator, respectively. The constant parameter α is the rate of exponential population growth for the prey, γ is the rate of exponential death for the predator, β is the rate at which the predators destroy the prey, and δ is the rate of predator population growth due to the consumption of prey. Inspired by the chemical law of mass action (Berryman, 1992), the Lotka-Volterra equations state that the rate of predation is directly proportional to the product of the populations of the prey and predator.
The Lotka-Volterra predator-prey model has several applications to economics and market dynamics. Richard Goodwin was one of the first to adopt the model to describe the cyclical relationship between employment and wages in economics, otherwise known as Goodwin’s class struggle model (Gandolfo, 2007). Other applications of generalized Lotka-Volterra systems in economics include the modeling of macroeconomic indicators (Sterpu et al. 2023), as well as wealth distributions in society, and values of firms in the stock market (Malcai et al. 2002).
In Fig. 3a, we simulate a system of Lotka-Volterra equations as defined in (6) with synthetic parameters α, β, γ, and δ. We then use OccamNet to fit (frac{dH}{dt}) and (frac{dL}{dt}) and simulate our generated differential equations using the same initial conditions. Our model is able to rediscover the exact functional form and constant parameters.
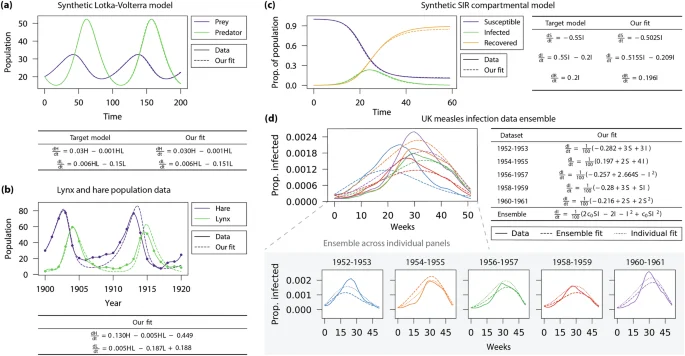
a Time-series plot of a simulated Lotka-Volterra predator-prey system. OccamNet was able to correctly reconstruct the functional form and constants with high accuracy. b Using cubic-spline interpolation, our system was able to learn the two differential equations from noisy, real-world data of lynx and hare populations with just 21 data points each. The inferred non-linear model can then be used to extend predictions of future populations. c The symbolic regression system is used to infer the SIR model of pandemic spread in synthetic data and d an ensemble of real-world measles infection data in the UK.
To validate our approach on a real-world dataset, we select the canonical example of the Hudson Bay Company’s data on the lynx and hare population in Canada from 1845–1935, which is known to align with the Lotka-Volterra model (MacLulich, 1937). As shown in Fig. 3b, we use the subset of records from 1900–1920 as it contains two population cycles with the least apparent noise. We additionally apply cubic-spline interpolation to reduce noise before fitting the numerically computed derivatives as discussed in Appendix A 2.
When fitting the interpolated data using OccamNet, we recover a system of ODEs that closely resembles the Lotka-Volterra equations. In particular, our model is able to learn the exponential population growth and decay terms αH and −γL, as well as the critical interaction terms of the form −βHL and δHL. Additionally, the best OccamNet fit includes small constant correction terms of −0.449 and 0.188. These constants have much smaller magnitudes relative to the other terms and may be due to over-fitting. A researcher may choose to either ignore these kinds of correction terms or to increase the level of constant regularization in OccamNet to obtain a fit with higher loss but potentially better generalizability.
OccamNet is, therefore, well positioned for the recovery of similar dynamical models in social science applications. For instance, future work could utilize OccamNet to analyze the dynamics between supply and demand in a market or between different sectors of the economy. Other types of data that may yield similar relationships include social mobility and income inequality data or political party dynamics.
Epidemic spread
Next, we use OccamNet to discover compartmental models of epidemics. In particular, we use synthetic and real datasets for the well-known Susceptible-Infected-Recovered (SIR) (Kermack and McKendrick, 1927) model for fixed population sizes, which is given by the ODE system
where s(t), i(t), and r(t) represent the proportions of the susceptible, infected, and recovered populations at time t respectively, and where s + i + r = 1.
The SIR model and numerous variants are often used to describe the spread of infectious diseases such as measles (Bjørnstad et al. 2002) or COVID-19 (Cooper et al. 2020). Such models are valuable for predicting the magnitude or duration of an epidemic, estimating epidemiological parameters such as the basic reproduction number (van den Driessche, 2017) (given by ({R}_{0}=frac{beta }{gamma }) in the SIR model), and forecasting the impact of public health interventions. Beyond modeling disease spread, SIR variants have also been used to study the diffusion of information on social networks (Kumar and Sinha, 2021; Woo and Chen, 2016), and thus carry substantial relevance to social science.
In Fig. 3c, we simulate a synthetic time series using the SIR model. OccamNet discovers the correct functional form of the SIR model along with approximately correct constant parameters up to rounding. The deviations of the learned constant parameters likely stem from higher-order errors in the numerical derivative estimate which are not addressed by the central difference formula. One could opt to use higher-order derivative approximations to account for such errors if necessary.
Since the SIR model is generally used to model disease spread, we evaluate OccamNet on a real-world panel dataset for measles infection data in the UK. This dataset also allows us to demonstrate the data ensemble learning functionality. Horrocks and Bauch used the SINDy (Sparse Identification of Nonlinear Dynamics) algorithm (Brunton et al. 2016) to fit a variant of the SIR model with time-varying contact rates to this measles dataset as well as to chickenpox and rubella data (Horrocks and Bauch, 2020). We note that SINDy requires the specification of a pre-set library of possible terms for which the algorithm learns sparse vectors of coefficients. OccamNet instead uses a specified library of simple bases to compose more complex terms with no additional inductive prior necessary. Our method requires less prior knowledge about the expression structure and is thus better suited to deriving new functional forms.
Horrocks and Bauch fit the entire measles time series to a singular equation for i(t) with time-varying β(t) (Horrocks and Bauch, 2020). We instead demonstrate OccamNet’s ability to discover the SIR model for each cycle of the epidemic with different β and γ parameters. Using a subset of the data from 1948–1958, we generate an ensemble of five measles incidence cycles. We then apply the denoising techniques as in (Brunton et al. 2016) and fit each dataset both individually and as an ensemble in which we learn the same functional form for all five datasets with varying constant parameters.
Figure 3d highlights the advantage of ensemble learning over individual fits. When each 2-year cycle is fit independently, OccamNet struggles to learn expressions with the SIR-like form of (frac{di}{dt}=beta is-gamma i). Due to the sparsity and noisiness of each individual dataset, it only extracts the interaction term βis from one of the five periods. The ensemble fit, however, discovers a function that includes the key form of βis—γi, as shown in the last row of the table in Fig. 3d. The parameter c0 is a placeholder for a constant that varies for each cycle. Ensemble learning can, therefore, help avoid over-fitting individual datasets and improve generalization. While our model also learns higher-order terms such as i2 and c0si2 for the ensemble, these terms are of much smaller magnitude compared to the leading terms and are thus of less importance to the correct fit. This is another example in which OccamNet’s custom regularization capabilities could be applied to eliminate higher-order terms.
Our experiments indicate that OccamNet offers a promising avenue for recovering compartmental models in various social science applications. For example, it can be used to develop models of the spread of information, beliefs, or trends across populations, akin to disease spread in public opinion or social media contexts. Similar transition dynamics may be present in the labor market (e.g., employment transitions) or in education (e.g., skill acquisition and loss). Formalizing these models symbolically would provide a more nuanced understanding of dynamic social processes, offering valuable insights for effective policy-making and strategic interventions.
Long-run economic growth
The final dynamical system we consider is the neoclassical Solow-Swan model of economic growth (Solow, 1956). The model postulates that long-run economic growth can be explained by capital accumulation, labor growth, and technological progress. The model typically assumes Cobb-Douglas-type aggregate production with constant returns to scale, given by
where y(t) is the output per unit of effective labor, k(t) is the capital intensity (capital stock per unit of effective labor), and α is the elasticity of output with respect to capital. The central differential equation in the Solow model describes the dynamics of k(t),
where s is the savings rate, n is the population growth rate, g is the technological growth rate, and δ is the capital stock depreciation rate. This equation states that the rate of change of capital stock is equal to the difference between the rate of investment and the rate of depreciation. The key result of the Solow growth model is that a greater amount of savings and investments do not affect the rate of economic growth in the long run.
While the Solow model was originally derived to describe U.S. economic growth, it has also been applied to other countries. If the model were perfectly universal, we would expect to see every country’s capital grow according to equation (9), with varying hidden parameters. We thus generate a synthetic example of country panel data for economic growth by simulating the Solow equations for k(t) and y(t), with the goal of rediscovering equation (9). As an additional level of complexity, we model the savings rate s and population growth rate n as time-dependent variables that grow according to the equations (frac{ds}{dt}=0.05) and (frac{dn}{dt}=0.05n). Each panel dataset is generated by randomly sampling initial conditions and parameters g and δ from uniform distributions of values outlined in Appendix B 6a. The resulting cross-country time series is displayed in Fig. 1. As demonstrated in the figure, OccamNet is able to recover the exact equation for (frac{dk}{dt}) (denoted as Output 1) with varying parameter c0 for each of the 20 synthetic panels.
We then attempt to fit the Solow model of capital growth to real-world, noisy country data. The input to our symbolic regression includes data on capital per capita, income per capita, savings rate, and population growth compiled by Khoo et al. (2021b), where it was utilized for regression under the Green Solow model—a variant of Solow-Swan for modeling sustainable growth (Brock and Taylor, 2004). Following the methodology of (Brock and Taylor, 2004), we select macro-economics data from 18 of the original 20 countries in the Organization for Economic Co-operation and Development (OECD) for which data was available. The k(t) data is originally sourced from the Penn World Tables (Feenstra et al. 2015), y(t) and n(t) are from the Maddison Project database (Maddison, 2017), and s(t) is from the World Development Indicators (World Bank, 2023). There is no available data for the remaining parameters g and δ, so they are instead treated as learnable constants. We also apply Savitzky-Golay filtering to smooth the data before running the regression, as described in Appendix B 6b.
In Fig. 4b, we compare the Solow-Swan model baseline to three expressions produced by OccamNet under increasing levels of complexity regularization. The Solow baseline is generated by finding the best-fit parameter c0 = g + δ in a least-squares of fit of equation (9). The expression with no regularization is given by (frac{dk}{dt}={c}_{1}left(frac{{k}^{2}}{y}+kright)-{c}_{2}) with constants c1 and c2 that vary across countries. While this expression has a lower weighted mean-squared error (WMSE) than the baseline, its functional form does not carry immediate economic intuition like the Solow model.
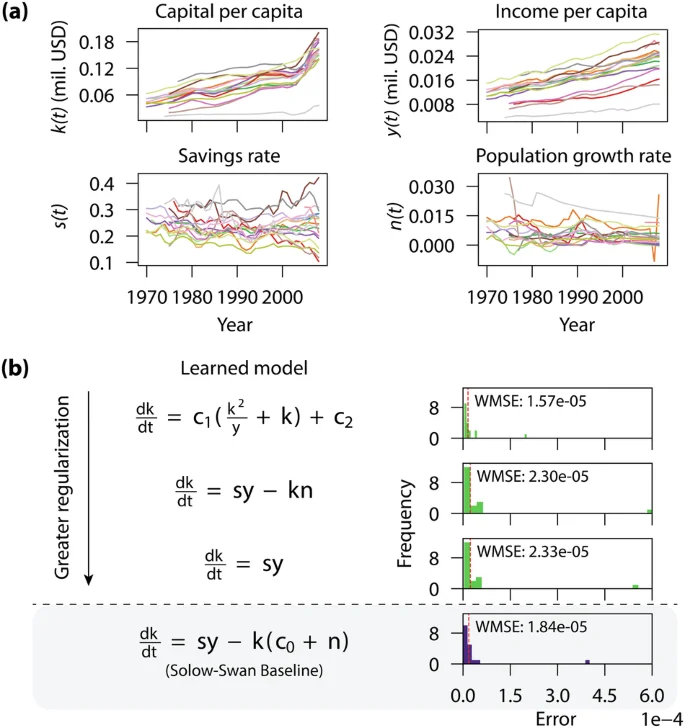
a Country-level macroeconomic data on capital and income per capita, savings rates, and population growth for 18 OECD member countries. b Ensemble learning of the Solow economic growth model. The error distribution of the differential equation, applied to each country, is shown for three expressions generated with increasing levels of complexity regularization. The identification of outliers may inform alternative explanations, hidden parameters, or higher-order corrections to the economic model.
We then add Constant Regularization as described in the Method section, which results in the equation (frac{dk}{dt}=sy-kn) closely matching the functional form of (9). This suggests that the Solow model has strong external validity as it can be discovered without any strong human priors. Finally, we apply Activation Regularization in addition to Constant Regularization, resulting in the output (frac{dk}{dt}=sy). The learned expression contains only one term from the Solow model and has the highest WMSE. The example in Fig. 4b concretely demonstrates the trade-off between accuracy and simplicity in the discovery of symbolic models. A researcher would thus benefit from running OccamNet with several specifications of regularization to select a result with the desired level of precision and complexity.
Discussion
This article aims to test and demonstrate the usefulness of neuro-symbolic methods in social science. We argue that its contribution is twofold. First, human-engineered quantitative models remain a critical part of social science research as they provide a way to formalize intuition or qualitative arguments about a social system and bridge micro-macro theories. Recognizing that neuro-symbolic methods help researchers benchmark these formal models against counterfactuals on the complexity-accuracy Pareto front: a practice not often done when new quantitative models are proposed. This is partly due to the difficulty of generating alternatives aside from baseline linear models or theories from the existing literature. The selection strategy of symbolic methods allows the intentional tuning of complexity (or meaningfulness, with human-aided post-selection) and prediction accuracy encountered by traditional parametric regression and deep learning methods.
Second, neuro-symbolic methods can also help social scientists discover new, interpretable models or generate novel hypotheses from data. Expressions on the Paretofront can be interpreted and tested without prejudice. Aside from complete models, terms that repeatedly appear along the front may also uncover persistent interactions Schmidt and Lipson (2009). Our proposed approach is powerful as it allows the user to tune the amount of inductive priors entered into the model. While models developed ab initio from a theoretical basis can be powerful in elucidating the implications of a present paradigm and incorporating human knowledge about human systems, the underconstrained nature of social science theories means that the researcher has to search through a vast space of potential candidates Hammersley and Gomm (1997); Healy (2017). Using neuro-symbolic regression, the user can opt to inject a minimal set of priors (e.g., provide a wide range of functional bases) or intentionally specify terms that existing theories may suggest.
Broadly speaking, two classes of quantitative models are typically employed in social science: parametric regression and non-parametric methods (Chen et al. 2019). Parametric regression has proven invaluable over the past few decades, particularly for its interpretability and data efficiency. However, its simplicity can obscure more complex behaviors, such as non-linear relationships or temporal dynamics. In contrast, non-parametric methods, including deep neural networks, are effective for capturing complex, non-linear patterns but lack interpretability, making them less useful for theory-building. We suggest that neuro-symbolic regression can offer a bridge between these two classes of statistical methods. In between specifying a complete model to let the system search for optimal parameters and leaving it open-ended to seek a parsimonious expression, the user can provide any amount of human insight. For instance, they may specify the presence of a power law relationship, an interaction term, or a derivative, and use the system to compose the rest of the model. Our case studies demonstrate each of these use cases and show that the framework can successfully help social scientists discover empirical regularities in the data with interpretable expressions.
Beyond interpretability, human-supplied biases are also useful in reducing the model search space, particularly when the problem faces a dearth of informative data. Since this is often the case in social science, we stress that the use of neuro-symbolic methods must be treated as a collaborative human-machine process in which a dictionary of motifs helps make inference problems tractable, as has been suggested by past work (Cardoso et al. 2020; Dominic et al. 2010). Humans also play a critical role in the validation and interpretation of the resulting models. Neuro-symbolic methods merely suggest functional fits; using these equations to paint a meaningful picture in the context of social science theory remains a human endeavor. The discovery of a formal model is often just the beginning, informing additional data collection, experiments, and qualitative inquiry (Epstein, 2008). A productive approach to quantitative social science needs to consider both the scientific and sociological role of modeling beyond its predictive capability alone.
Neuro-symbolic regression has significant potential as a powerful tool for hypothesis creation and model discovery in social science. Our approach successfully rediscovered well-established models, such as the Cobb-Douglas production function and the Lotka-Volterra equations, demonstrating its ability to capture key underlying relationships. This validation of known models indicates that our framework could effectively identify new patterns and generate hypotheses when applied to novel datasets. One limitation of our framework is its dependence on user-specified inductive priors, which may introduce bias into the discovery process. Further research could focus on developing more adaptive techniques for integrating domain expertise while maintaining the objectivity of machine-driven model discovery. Moreover, as our current approach has been tested primarily on smaller datasets, exploring its scalability to larger, more complex datasets will be an important area for future work.
An exciting next step would be to collaborate with social scientists in applying OccamNet to their research, particularly to datasets that are conjectured to capture a symbolic law. In problems with more available data and multiple independent panels, a machine learning approach allows data to be divided into training and validation sets—provided that unexplained errors between the two sets are uncorrelated—to improve the out-of-distribution performance or external validity, of the learned model. We hope to see our proposed human-machine framework applied to unearth entirely new quantitative or formal models. Furthermore, OccamNet’s flexibility in incorporating user-defined bases such as piecewise functions and logical operators allows for moving beyond learning arithmetic expressions. Future work could include applying OccamNet to learn more complex symbolic rules such as strategies in economic games (Duffy and Engle-Warnick, 2002) or network-structured models.
Data availability
The dataset for the HEP-TH citation network is publicly available online at https://snap.stanford.edu/data/cit-HepTh.html (Leskovec and Krevl, 2014; Leskovec et al. 2005). The Wikipedia hyperlink network data is available from the Network Repository at https://networkrepository.com/web-wikipedia-link-en13-all.php (Rossi and Ahmed, 2015; Various, 2009). A compilation of the 1928 Cobb-Douglas dataset (Cobb and Douglas, 1928) is available at http://web.mit.edu/pjdavis/www/options/cobbdouglas.xls. MacLulich’s 1937 compilation of the Hudson Bay Company’s lynx-hare dataset (MacLulich, 1937) is available online at http://people.whitman.edu/~hundledr/courses/M250F03/M250.html. The UK measles infection data is available at https://math.mcmaster.ca/~bolker/measdata.html. The compiled dataset for the Solow-Swan model experiments is available at https://github.com/zykhoo/nODE-Solow (Khoo et al. 2021a).
Code availability
The datasets generated during and/or analyzed during the current study are available at https://github.com/druidowm/OccamNet_SocialSci.
Notes
-
Expression depth is defined as the maximum number of nested operations.
-
The central difference formula is given by ({f}^{{prime} }(x)approx left(f(x+h)-f(x-h)right)/2h) and accounts for second-order error in the derivative approximation.
References
-
Albert R (2005) Scale-free networks in cell biology. J Cell Sci 118(21):4947–4957
Google Scholar
-
Albert R, Jeong H, Barabási A-L (1999) Diameter of the world-wide web. Nature 401(6749):130–131
Google Scholar
-
Barabási A-L, Albert R (1999) Emergence of scaling in random networks. Science 286(5439):509–512
Google Scholar
-
Berryman AA (1992) The orgins and evolution of predator-prey theory. Ecology 73(5):1530–1535
Google Scholar
-
Biddle J (2012) Retrospectives: the introduction of the Cobb-Douglas regression. J Econ Perspect 26(2):223–236
Google Scholar
-
Biggio L, Bendinelli T, Neitz A, Lucchi A, Parascandolo G (2021) Neural symbolic regression that scales In: Marina Meila and Tong Zhang 0001, editors, Proceedings of the 38th International Conference on Machine Learning, ICML 2021, 18–24 July 2021, Virtual Event, volume 139 of Proceedings of Machine Learning Research, pages 936–945. PMLR, http://proceedings.mlr.press/v139/biggio21a.html
-
Bjørnstad ON, Finkenstädt BF, Grenfell BT (2002) Dynamics of measles epidemics: estimating scaling of transmission rates using a time series SIR model. Ecol Monogr 72(2):169–184
Google Scholar
-
Brock WA, Taylor MS (2004) The Green Solow Model. Working Paper 10557, National Bureau of Economic Research, https://www.nber.org/papers/w10557 June. Series: Working Paper Series
-
Broido AD, Clauset A (2019) Scale-free networks are rare. Nat Commun 10(1):1017
Google Scholar
-
Brunton SL, Proctor JL, Kutz JN (2016) Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc Natl Acad Sci 113(15):3932–3937
Google Scholar
-
Cardoso P, Branco VV, Borges PAV, Carvalho JC, Rigal F, Gabriel R, Mammola S, Cascalho J, Correia L (2020) Automated discovery of relationships, models, and principles in ecology. Front Ecol Evol 8:530135
Google Scholar
-
Chatterjee A, Mitrović M, Fortunato S (2013) Universality in voting behavior: an empirical analysis. Sci Rep 3(1):1049
Google Scholar
-
Chen Y, Angulo MT, Liu Y-Y (2019) Revealing complex ecological dynamics via symbolic regression. BioEssays 41(12):1900069
Google Scholar
-
Clauset A, Shalizi CR, Newman MEJ (2009) Power-law distributions in empirical data. SIAM Rev 51(4):661–703
Google Scholar
-
Cobb CW, Douglas PH (1928) A theory of production. Am Econ Rev 18(1):139–165
Google Scholar
-
Cooper I, Mondal A, Antonopoulos CG (2020) A SIR model assumption for the spread of COVID-19 in different communities. Chaos Soliton Fract 139:110057
Google Scholar
-
Costa A, Dangovski R, Dugan O, Kim S, Goyal P, Soljačić M, Jacobson J (2021) Fast neural models for symbolic regression at scale. http://arxiv.org/abs/2007.10784
-
Cranmer M, Sanchez Gonzalez A, Battaglia P, Xu R, Cranmer K, Spergel D, Ho S (2020) Discovering symbolic models from deep learning with inductive biases. In: Advances in neural information processing systems, volume 33, pages 17429–17442. Curran Associates, Inc.,
-
Dominic P, Leahy D, Willis M (2010) Gptips: an open source genetic programming toolbox for multigene symbolic regression. Lecture Notes in Engineering and Computer Science, 2180, 12
-
Douglas PH (1976) The Cobb-Douglas production function once again: its history, its testing, and some new empirical values. J Polit Econ 84(5):903–915
Google Scholar
-
Duffy J, Engle-Warnick J (2002) Using symbolic regression to infer strategies from experimental data. In: Shu-Heng Chen, editor, Evolutionary Computation in Economics and Finance, Studies in Fuzziness and Soft Computing, pages 61–82. Physica-Verlag HD, Heidelberg, https://link.springer.com/chapter/10.1007/978-3-7908-1784-3_4
-
Epstein JM (2008) Why Model? J Artif Soc Soc Simul 11(4), https://www.jasss.org/11/4/12.html
-
Feenstra RC, Inklaar R, Timmer MP (2015) The next generation of the penn world table. Am Econ Rev 105(10):3150–82
Google Scholar
-
Gabaix X (1999) Zipf’s law for cities: an explanation. Q J Econ 114(3):739–767
Google Scholar
-
Gailmard S, Patty JW (2012) Formal models of bureaucracy. Annu Rev Polit Sci 15(1):353–377
Google Scholar
-
Gandolfo G (2007) The Lotka-Volterra equations in economics: an italian precursor. Econ Polit XXIV:343–348
-
Gavish M, Donoho DL (2014) The optimal hard threshold for singular values is (4/sqrt{3}). IEEE Trans Inf Theory 60(8):5040–5053
Google Scholar
-
Gehrke J, Ginsparg P, Kleinberg J (2003) Overview of the 2003 KDD cup. ACM SIGKDD Explor Newsl 5(2):149–151
Google Scholar
-
Gleich DF, Rossi RA (2014) A dynamical system for PageRank with time-dependent teleportation. Internet Math 1–30
-
Granovetter M (1978) Threshold models of collective behavior. Am J Sociol 83(6):1420–1443
Google Scholar
-
Guimerà R, Reichardt I, Aguilar-Mogas A, Massucci FA, Miranda M, Pallarès J, Sales-Pardo M (2020) A bayesian machine scientist to aid in the solution of challenging scientific problems. Sci Adv 6(5):eaav6971
Google Scholar
-
Hammersley M, Gomm R (1997) Bias in social research. Sociol Res Online 2(1):7–19
Google Scholar
-
Healy K (2017) Fuck nuance. Sociol Theory 35(2):118–127
Google Scholar
-
Holt S, Qian Z, Schaar M (2023) Deep generative symbolic regression. ArXiv, https://doi.org/10.48550/arXiv.2401.00282
-
Horrocks J, Bauch CT (2020) Algorithmic discovery of dynamic models from infectious disease data. Sci Rep 10(1):7061
Google Scholar
-
Kamienny P-A, d’Ascoli S, Lample G, Charton F (2022) End-to-end symbolic regression with transformers. In: Advances in Neural Information Processing Systems, https://openreview.net/forum?id=GoOuIrDHG_Y Edited by Alice H. Oh, Alekh Agarwal, Danielle Belgrave, and Kyunghyun Cho
-
Keohane RO, King G, Verba S (2021) Designing social inquiry: scientific inference in qualitative research. Princeton University Press, Princeton, new edition edition. ISBN 978-0-691-22462-6 978-0-691-22463-3
-
Keren LS, Liberzon A Lazebnik TA (2023) computational framework for physics-informed symbolic regression with straightforward integration of domain knowledge. Sci Rep 13(1), https://doi.org/10.1038/s41598-023-28328-2
-
Kermack WO, McKendrick AG (1927) A contribution to the mathematical theory of epidemics. Proc R Soc Lond Ser A Contain Pap A Math Phys character 115(772):700–721
Google Scholar
-
Khoo Z-Y, Lee KH, Huang Z, Bressan S (2021a) Neural ordinary differential equations for the regression of macroeconomics data under the green solow model. In Database and Expert Systems Applications: 32nd International Conference, DEXA 2021, Virtual Event, September 27–30, 2021, Proceedings, Part I 32, pages 78–90. Springer,
-
Khoo Z-Y, Lee KH, Huang Z, Bressan S (2021b) Neural ordinary differential equations for the regression of macroeconomics data under the green solow model. In: Christine Strauss, Gabriele Kotsis, A. Min Tjoa, and Ismail Khalil, eds. Database and Expert Systems Applications, Lecture Notes in Computer Science, pages 78–90, Cham, https://doi.org/10.1007/978-3-030-86472-9_7. Springer International Publishing. ISBN 978-3-030-86472-9
-
Kleinberg J, Ludwig J, Mullainathan S, Obermeyer Z (2015) Prediction policy problems. Am Econ Rev 105(5):491–495
Google Scholar
-
Kubalık J, Derner E, Babuška R (2023) Neural networks for symbolic regression. ArXiv, abs/2302.00773, https://doi.org/10.48550/arXiv.2302.00773
-
Kumar P, Sinha A (2021) Information diffusion modeling and analysis for socially interacting networks. Soc Netw Anal Min 11(1):11
Google Scholar
-
Leskovec J, Krevl A (2014) SNAP Datasets: stanford large network dataset collection. http://snap.stanford.edu/data
-
Leskovec J, Kleinberg J, Faloutsos C (2005) Graphs over time: densification laws, shrinking diameters and possible explanations. In: Proceeding of the eleventh ACM SIGKDD international conference on Knowledge discovery in data mining – KDD ’05, page 177, Chicago, Illinois, USA, https://doi.org/10.1145/1081870.1081893. ACM Press. ISBN 978-1-59593-135-1. http://portal.acm.org/citation.cfm?doid=1081870.1081893
-
Liu J, Guo S (2023) Symbolic regression in financial economics. The First Tiny Papers Track at ICLR 2023, https://openreview.net/forum?id=RuCQRXk7a7G
-
Liu S, Li Q, Shen X, Sun J, Yang Z (2024) Automated discovery of symbolic laws governing skill acquisition from naturally occurring data. Nat Comput Sci 4(5):334–345
Google Scholar
-
Lotka AJ (1910) Contribution to the theory of periodic reactions. J Phys Chem 14(3):271–274
Google Scholar
-
MacLulich, DA (1937) Fluctuations in the numbers of the varying hare (Lepus Americanus). University of Toronto Press, http://www.jstor.org/stable/10.3138/j.ctvfrxkmj. ISBN 978-1-4875-8178-7
-
Maddison, A (2017) Maddison database 2010, https://www.rug.nl/ggdc/historicaldevelopment/maddison/releases/maddison-database-2010
-
Malcai O, Biham O, Richmond P, Solomon S (2002) Theoretical analysis and simulations of the generalized Lotka-Volterra model. Phys Rev E 66(3):031102
Google Scholar
-
Martin BT, Munch SB, Hein AM (2018) Reverse-engineering ecological theory from data. Proc R Soc B: Biol Sci 285(1878):20180422
Google Scholar
-
Nelder JA, Mead R (1965) A simplex method for function minimization. Comput J 7(4):308–313
Google Scholar
-
Nelder JA, Wedderburn RWM (1972) Generalized linear models. J R Stat Soc Ser A 135(3):370
Google Scholar
-
Oliver PE (1993) Formal models of collective action. Annu Rev Sociol 19(1):271–300
Google Scholar
-
Pan X, Uddin MK, Ai B, Pan X, Saima U (2019) Influential factors of carbon emissions intensity in OECD countries: evidence from symbolic regression. J Clean Prod 220:1194–1201
Google Scholar
-
Petersen BK, Larma ML, Mundhenk TN, Santiago CP, Kim SK. Kim JT (2021) Deep symbolic regression: Recovering mathematical expressions from data via risk-seeking policy gradients. In: International Conference on Learning Representations, https://openreview.net/forum?id=m5Qsh0kBQG
-
Ranganathan S, Spaiser V, Mann RP, Sumpter DJT (2014) Bayesian dynamical systems modelling in the social sciences. PLoS One 9(1):e86468
Google Scholar
-
Ranganathan S, Nicolis SC, Spaiser V, Sumpter DJT (2015) Understanding democracy and development traps using a data-driven approach. Big Data 3(1):22–33
Google Scholar
-
Rossi RA, Ahmed NK (2015) The network data repository with interactive graph analytics and visualization. In: AAAI, https://networkrepository.com
-
Rudin LI, Osher S, Fatemi E (1992) Nonlinear total variation based noise removal algorithms. Phys D: Nonlinear Phenom 60(1–4):259–268
Google Scholar
-
Schmidt M, Lipson H (2009) Distilling free-form natural laws from experimental data. Science 324(5923):81–85
Google Scholar
-
Solow RM (1956) A contribution to the theory of economic growth. Q J Econ 70(1):65
Google Scholar
-
Spaiser V, Hedström P, Ranganathan S, Jansson K, Nordvik MK, Sumpter DJT (2018) Identifying complex dynamics in social systems: a new methodological approach applied to study school segregation. Sociol Methods Res 47(2):103–135
Google Scholar
-
Stenseth NC, Falck W, Bjørnstad ON, Krebs CJ (1997) Population regulation in snowshoe hare and Canadian lynx: asymmetric food web configurations between hare and lynx. Proc Natl Acad Sci 94(10):5147–5152
Google Scholar
-
Sterpu M, Rocşoreanu C, Soava G, Mehedintu A (2023) A generalization of the grey lotka–volterra model and application to GDP, export, import and investment for the european union. Mathematics 11(15):3351
Google Scholar
-
Swan TW (1956) Economic growth and capital accumulation. Econ Rec 32(2):334–361
Google Scholar
-
Truscott P, Korns MF (2014) Explaining unemployment rates with symbolic regression. In: Rick Riolo, Jason H. Moore, and Mark Kotanchek, editors, Genetic Programming Theory and Practice XI, pages 119–135. Springer New York, New York, NY, https://doi.org/10.1007/978-1-4939-0375-7_7. ISBN 978-1-4939-0374-0 978-1-4939-0375-7. Series Title: Genetic and Evolutionary Computation
-
Udrescu S-M, Tegmark M (2020) AI Feynman: a physics-inspired method for symbolic regression. Sci Adv 6(16):eaay2631
Google Scholar
-
van den Driessche P (2017) Reproduction numbers of infectious disease models. Infect Dis Model 2(3):288–303
Google Scholar
-
Various. Wikipedia database dump, http://en.wikipedia.org/wiki/Wikipedia:Database_download (2009). Version from 2009-03-06
-
Wang Y, Wagner N, Rondinelli JM (2019) Symbolic regression in materials science. MRS Commun 9(3):793–805
Google Scholar
-
Woo J, Chen H (2016) Epidemic model for information diffusion in web forums: experiments in marketing exchange and political dialog. SpringerPlus 5(1):66
Google Scholar
-
World Bank (2023) Development Indicators ∣ DataBank, https://databank.worldbank.org/source/world-development-indicators
-
Yang G, Li X, Wang J, Lian L, Ma T (2015) Modeling oil production based on symbolic regression. Energy Policy 82:48–61
Google Scholar
-
Zellner A (1984) Basic issues in econometrics. University of Chicago Press, Chicago. ISBN 978-0-226-97983-0
Acknowledgements
We would like to thank Megan Yamoah for useful discussions during the drafting of this article. This work was sponsored in part by the United States Air Force Research Laboratory and the United States Air Force Artificial Intelligence Accelerator and was accomplished under Cooperative Agreement Number FA8750-19-2-1000. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the United States Air Force or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. This work was also sponsored in part by the National Science Foundation under Cooperative Agreement PHY-2019786 (The NSF AI Institute for Artificial Intelligence and Fundamental Interactions, http://iaifi.org/) and in part by the Air Force Office of Scientific Research under the award number FA9550-21-1-0317.
Author information
Authors and Affiliations
Contributions
Conceptualization, visualization, and writing—original draft: JB, SH; methodology: JB, OD; investigation: JB; Supervision: RD, MS; writing—review and editing: JB, SH, OD, RD, MS. Correspondence to JB.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
This article does not contain any studies with human participants performed by any of the authors.
Informed consent
This article does not contain any studies with human participants performed by any of the authors.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Appendix
OccamNet code
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and permissions
About this article
Cite this article
Balla, J., Huang, S., Dugan, O. et al. AI-assisted discovery of quantitative and formal models in social science.
Humanit Soc Sci Commun 12, 114 (2025). https://doi.org/10.1057/s41599-025-04405-x
-
Received: 29 August 2023
-
Accepted: 20 January 2025
-
Published: 31 January 2025
-
DOI: https://doi.org/10.1057/s41599-025-04405-x