Abstract
Present research work deals with the extremely sensitive pressure-sensing capabilities of defective one-dimensional photonic crystal structure (GaP/SiO2)N/Al2O3/(GaP/SiO2)N. The proposed structure is realized by putting a defective layer of material Al2O3 in the middle of a structure consisting of alternating layers of GaP and SiO2. The transfer matrix method has been employed to examine the transmission characteristics of the proposed defective one-dimensional photonic crystal in addition to MATLAB software. An external application of the hydrostatic pressure on the proposed structure is responsible for the change in the position and intensity of defect mode inside the photonic band gap of the structure due to pressure-dependent refractive index properties of the materials being used in the design of the sructure. Additionally, the dependence of the transmission properties of the structure on other parameters like incident angle and defect layer thickness has also studied. The theoretical obtained numeric values of the quality factor and sensitivity are 17,870 and 72 nm/GPa respectively. These results are enough to support our claim that the present design can be used as an ultra-sensitive pressure sensor.
Introduction
Pioneering research work on the photonic crystals (PhCs) was first carried out by Yablonovitch and John in 1987. They have articulated their architecture by considering a periodic arrangement of dielectric materials which may be in one-dimensional (1d), two-dimensional (2d), and three-dimensional (3d) as a 1d, 2d and 3d PhCs respectively1,2. The extensive research work on PhCs has been done so far. The present involvement of PhCs into variety of modern applications makes them suitable to be used as a promising candidate in research fields governing optical, chemical and medical engineering. PhCs have tremendous ability of restricting the propagation of electromagnetic waves of specific frequencies passing through them. This specific frequency range is called as photonic bandgap (PBG)3. The introduction of defects like cavities either by changing the thickness or material of the structure may bring sharp transmission peak inside PBG. Such modified structures are called as defective photonic crystals (DPhCs)4. One of the most suitable application of DPhCs is to use them as a chemical, biofluid or optical sensing structures. The easier fabrication techniques associated with 1d photonic structures allow them to be used as a most effective sensing structures due to their minute sensing and detection capabilities5. Many peculiar applications of 1d DPhCs related to biochemistry6, medical science7,8,9,10,11,12,13,14, petroleum engineering9,15,16,17,18,19, and other branches of sciences20,21,22,23,24,25,26,27,28 have been explored by the researchers recently. The photonic biosensors made up of 1d DPhCs have revolutionized the designing, development and testing methodology of biosensors due to significantly improved performance of such structures in terms of sensitivity (S), figure-of-merit (FoM), quality factor (Q) and detection limit (DL)29,30,31,32,33,34,35,36. Actually, 1d DPhCs based photonic biosensors improve the interaction time between incident photon and the target matter precured inside sensing zone of the structure for accomplishment of high-field localization. The effects of interference, phase and group birefringence associated with the biosensors composed of 2d DPHCs restrict their fabrication whereas the fascinating properties like tunable dispersion and birefringence, homogeneous and isotropic behavior of the structure and the devise compatibility makes the fabrication of 1d DPhCs biosensor easier. Such structures can be easily fabricated by adopting suitable thin film deposition techniques depending upon the choice of the materials used in the design.
The present research work is based on the photo-elastic phenomenon under the influence of the stress applied over 1d DPhC (GaP/SiO2)N/Al2O3/(GaP/SiO2)N. The application of stress over the structure disturbs the isotropic and homogeneous nature of the refractive indices of the contitutent materials which induces the ultra high pressure sensing capabilities into 1d DPhC composed of (GaP/SiO2)N/Al2O3/(GaP/SiO2)N. The architectural details along with the theoretical formulation of the structure is discussed in Section “Theoretical formulation”. Results of the work are presented in Section “Results and discussion”. Finally, conclusions are summarized in Section “Conclusion”.
Theoretical formulation
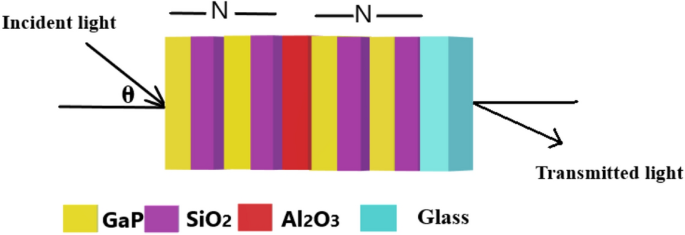
The transfer matrix method (TMM) has been employed to investigate the theoritical findings of the 1d DPhC composed of (GaP/SiO2)N/Al2O3/(GaP/SiO2)N as shown in Fig. 1. The present structure can be fabricated by depositing the alternating periodic layers of gallium phosphide (GaP) and fused silica (SiO2) of period number N on either side of an additional defect layer of alluminium oxide (Al2O3) located at the middle of the structure over glass substarte. The transfer matrix approach connencting the electric and magnetic fileds of electromagnetic wave propagating into the structure near to the interface conneting every two adjesesnt layers of the structure as defined in Eq. (1) below25,26,27,28

Systametic view of the propoed 1d DPhC composed of (GaP/SiO2)N /Al2O3/(GaP/SiO2)N. The yellow, pink, red and cyan colours are representing different layers of the structure made up of GaP, SiO2, Al2O3 and glass materials respectively.
Here M11, M12, M21 and M22 are representing the elements of the resultant transfer matrix M of the structure. The symbols (mathfrak{M})1, (mathfrak{M})2 and (mathfrak{M})d are representing the characteristic matrix of material layers GaP, SiO2 and Al2O3 of the structure. The subscripts 1, 2 and d are being used material layers GaP, SiO2 and Al2O3 respectively of the structure. The characteristic matrix (mathfrak{M}) n (n = 1, 2 and d) of any nth layer of the structure can be defined as
The reflection (r) and transmission (t) coefficients of the proposed structure (GaP/SiO2)N/Al2O3/(GaP/SiO2)N are defined by
The reflectance (R) and transmittance (T) of the structure can be with the help of following relation (4)
Here p0 = n0 cos(θ0) and ps = ns cos(θs) are admittances of input and output ends of the structure respectively, corresponding to s-polarized wave. For p-polarized wave, input and output admittances would be p0 = cos(θ0)/n0 and ps = cos(θs)/ns respectively. The symbols θ0 and θs are denoting angles of incidence and emergence at input and output ends of the structure respectively.
The hydrostatic pressure applied externally over the structure (GaP/SiO2)N/Al2O3/(GaP/SiO2)N made up of acousto-optic materials can be easily measured due to change in the refractive indices of the constituent materials used in the designing of the present structure. The change in characteristics properties of the acousto-optic materials employed in the proposed pressure sensing design can be observed with the help of stress–strain formulas under the influence of externally applied pressure on the structure. This pressure over the structure is enough to affect the refractive index of the material with stress due to photo-elastic phenomenon which in turn affects the optical performance of the structure. The stress (σ) is like a pressure which determines the force acting per unit area and can be decomposed into nine components forming a secon-rank stress tensor (σij). Here combination of the subscripts i and j is used to represesnt different combinations of x, y and z axes depending upon the direction of the force applied over the respective areas of the structure. The relation between the direction dependent refractive index (nij) and the stress tensor (σij) for a cubic media can be expressed as
The σij is the stress applied over any ij plane of a cubic crystal resulting a corresponding change in the refractive index of the material denoted as nij. If the pressure applied on the structure from only one direction with respect to normal on the plane of the structure, the whole device is said to under stress. In this condition, ({sigma }_{xx}) = ({sigma }_{yy}) = ({sigma }_{zz}) = σ and ({sigma }_{xy}) = ({sigma }_{yz}) = ({sigma }_{zx}) = 0. Under this condition the stress state is said to be in-plan due to stress anisotropy effect resulting a refractive index of the medium as (n={n}_{0}-({C}_{11}+2{C}_{12})sigma). Here n0 is the refractive index in absence of stress.
The stress-optic constants, Ck (k = 1, 2, 3) used in the above relation (5) are defined as
Here alphabets E, G, and V are representing young’s modulus, shear modulus, and Poisson’s ratio respectively. The strain-optic constants are being shown by notations p11, p12 and p44. For isotropic crystals they are mutually connected as
Results and discussion
This section deals with the performance of the suggested pressure sensing photonic structure which is the main objective of the work. The thickness of alternating periodic layers of materials GaP and SiO2 of the proposed structure 115 nm and 273 nm respectively. The thickness of the defect layer of material Al2O3 is 255 nm located at middle of the structure shown in Fig. 1. All the layers of the proposed pressure sensing structure is made up of elasto-optic materials GaP, SiO2 and Al2O3. The period number N of the structure has been fixed to 5. The numeric values of stress-optic (Ck) and strain-optic (pij) constants associated with the materials GaP, SiO2 and Al2O3 are given in Table 1 below.
First transmission spectra under normal incidence in absence of an external pressure has been computed by using MATLAB programing in addition to TMM as shown in Fig. 2. It exhibits a single defect mode of transmittance 88% located at 1660.24 nm inside PBG extending from 1281.6 to 2244.6 nm as shown in Fig. 2. This defect mode arises inside PBG of the structure due to insertion of an additional layer of Al2O3 of thickness 255 nm which disturbs the periodicity of the structure. Next efforts have been given to analyze the effect of pressure applied externally on the structure. This analysis makes us aware about the pressure sensing capabilities of our structure due to presence of elasto-optic materials in the design.

Transmittance of proposed structure (GaP/SiO2)N /Al2O3/(GaP/SiO2)N under normal incidence in absence of an external pressure (0 GPa).
Effect of pressure on the performance of the proposed sensor
In this section, we have examined how the position and intensity of the defect mode inside PBG of the proposed 1d DPhC (GaP/SiO2)N /Al2O3/(GaP/SiO2)N is affacted under the influence of an external pressure which varies from 0 GPa to 2.0 GPa in steps of 0.5 GPa. This purpose is acommplished by applying the pressure 0.5, 1.0, 1.5 and 2.0 GPa seperalely on the structure along the priodicity of the structure and obserbed the respective changes on the transmission spectra of structure as shown in Fig. 3. It shows five transmission peaks of black, red, blue, pink and green colours inside PBG of the structure corresponding to externally applied pressure of values 0, 0.5, 1.0, 1.5 and 2.0 GPa respectively. One can easily observe that the defect mode is started to shift towards higher wavelength side as the pressure increases. The maximum shifting in the position of defect mode is observed corresponding to pressure 2.0 GPa. Though the application of an external pressure on the structure reduces the intensity of the defect mode inside PBG of the proposed structure from 88 to 80.79% as the pressure increases from 0 to 2.0 GPa. This reduction in the intensity of the defect mode inside PBG due to incerese in pressure is sufficient to be examined by the optical spectrum analyzer available for the purpose. Actually, application of external pressure on the structure increases the refractive index of the defect layer made up of material Al2O3 due to elasto-optic effect (Table 2) responsible for the shifting of defect mode inside PBG. Moreover external pressure on the structure creates the pressure dependent imperfactions in the material which are responsible for scattering losses which results decrease in the intensity of the defect mode inside PBG. These imperfactions reach to maximum under the pressure 2.0 GPa resulting the maximum drop in the intensity of defect mode as shown in Fig. 3.

Transmittance of proposed structure (GaP/SiO2)N /Al2O3/(GaP/SiO2)N under normal incidence corresponding to external pressure. The transmittance peaks of colours black, red, blue, pink and green are corresponding to external pressure 0, 0.5, 1.0, 1.5 and 2.0 GPa respectively.
The linear curve fitting has been applied on to data presented in Table 2 for getting pictorial representation. The curve fitting results are shown in Fig. 4 below. It shows the perfect linear relationship between the external pressure dependent refractive index values of Al2O3 material layer responsible for creating defect. Aforementioned linear shifting of refractive index (nd) of Al2O3 dependent upon external pressure (P) is fitted with following curve fitting as

External pressure dependent refractive index values of Al2O3 are shown by green colour solid balls and red colour solid line is showing the linear curve fitting applied over the data.
Here R2 is the corellation factor which high as expected.
Effect of defect layer thickness on the performance of the proposed sensor
Next, efforts have been further extended to examine the pressure sensing capabilities of different pressure sensors of defect layer thicknesses dd = 100 nm, dd = 200 nm, dd = 300 nm and dd = 400 nm, each under the influence of external pressure 0.5 GPa, 1.0 GPa, 1.5 GPa and 2.0 GPa with respect to absence of an external pressure applied over the structures. The purpose of this additional work is to identify the most sensitive structure amongst all the pressure sensing 1d DPhC structure considered in this study. This time we have calculated the sensitivity of each structures of defect layer thickness dd = 100 nm, dd = 200 nm, dd = 300 nm and dd = 400 nm under the influence of external pressure 0.5, 1.0, 1.5 and 2.0 GPa with respect to absence of an external pressure applied over the structures. The sensitivity (S) of the pressure sensor is one of the most significant parameters which determines how minutely and accurately our sensor can sense the change in the defect mode position (Δλ) inside PBG of the structure with respect to change in the external pressure (ΔP) applied over the structure. For our structure sensitivity can be defined as
Next, transmittance of all four pressure sensors of defect layer thickness 100, 200, 300 and 400 nm, each under the influence of external pressure 0, 0.5, 1.0, 1.5 and 2.0 GPa have been plotted separately in Fig. 5 below. These transmittance plots are the mandatory requirement to calculate the sensitivity of each structures under the influence of an external pressure. It is evident from Fig. 5 that as the thickness of defect layer of each structure increases from 100 to 400 nm, pressure dependent defect modes inside PBGs of the structures of defect layer thickness 100, 200, 300 and 400 nm shown in blue, red, yellow, violet and green colours corresponding to external pressure 0, 0.5, 1.0, 1.5 and 2.0 GPa respectively have red shift. Moreover, their full width half maximum (FWHM) also improves which is an indicator for identifying the most sensitivity structures. Any increase in the thickness of defect layer beyond 400 nm pushes the pressure dependent defect modes outside the PBG extending from 1281.6 to 2244.6 nm as shown in Fig. 2 which is against the working principle of the photonic biosensors.

Transmittance of proposed structure (GaP/SiO2)N/Al2O3/(GaP/SiO2)N of defect layer thickness (a) dd = 100 nm, (b) dd = 200 nm, (c) dd = 300 nm and (d) dd = 400 nm, under normal incidence corresponding to different external pressures. The transmittance peaks of colours blue, red, yellow, violet and green are corresponding to external pressure 0 GPa, 0.5, 1.0, 1.5 and 2.0 GPa respectively.
The sensitivity of all four structures of defect layer thickness 100, 200, 300 and 400 nm under the influence of fixed external pressure 0.5 GPa has been calculated by using Eq. (9) with the help of Fig. 5a, b, c and d respectively. The sensitivity values of all four structures are listed in Table 3 below.
The sensitivity calculated data presented in the Table 3 shows that the 1d DPhC with defect layer thickness 400 nm is the most sensitivity pressure sensing structure which gives a sensitivity of 50 nm/GPa. The numeric data giving defect layer thickness dependent sensitivity of the structure under the influence of fixed external pressure of 0.5 GPa as mentioned in Table 3 has been plotted in Fig. 6 below. It shows that the linear relationship between defect layer thickness of the structures and their sensitivity values for the structure with dd = 100, 200 and 300 nm. But for the structure with dd = 400 nm the restricted increase in the sensitivity of 50 nm/GPa is noticed which reaches to semi-steady state.

A direct relationship between the sensitivity and defect layer thickness of the structures under the influence of fixed external pressure of 0.5 GPa.
Effect of angle of incidence on the performance of the proposed sensor
After getting optimized thickness of the defect layer dd = 400 nm to design a pressure sesnor of maximum sesntivity of 50 nm/GPa under normal incidence, we have focused ourself to study the effect of change in angle of incidence (θ0) from normal incidence (θ0 = 0°) to oblique incidence (θ0 ≠ 0°) and observe the respective change on the senstivity of the 1d DPhC with optimized defect layer thickness dd = 400 nm. For this purpose the transmittance spectra of the photonic pressure sesning structure (GaP/SiO2)N/Al2O3/(GaP/SiO2)N with dd = 400 nm have been recorded at different incident angles θ0 = 0°, 20°, 40° and 60° as shown in Fig. 7a, b, c and d respectively. It has been noticed in Fig. 7 that as angle of incidence approaches from normal to oblique incidence condition, the externally applied pressure dependent defect modes inside PBG of the structure have blue shift with reduction in the intensity of the defect modes. This reduction in the intensity of the defect mode is due to enhancement in the reflectivity of the structure under oblique incidence. The condition of oblique incidence reduces the FWHM of each defect modes both in absence and presence of an external pressure applied over the structure. This reduction in the FWHM of the pressure influenced defect modes is more meaning full as compare to reduction in the intensity. The reduction in the intensity of the defect mode is from 91 to 71% as θ0 changes from 0 to 60° respectively under external pressure of 0.5 GPa as evident from Fig. 7. Moreover this reduction in the intensity is well above the threshhold value of the energy requirement of the electronic detectors used for the purpose.

Transmittance of proposed structure (GaP/SiO2)N /Al2O3/(GaP/SiO2)N of defect layer thickness dd = 400 nm with (a) θ0 = 0°, (b) θ0 = 20°, (c) θ0 = 40° and (d) θ0 = 60° corresponding to different external pressures. The transmittance peaks of colours blue, red, yellow, violet and green are corresponding to external pressure 0, 0.5, 1.0, 1.5 and 2.0 GPa respectively.
The information obtained from Fig. 7 has been utilized for calculating sesntivity of the structure with dd = 400 nm at θ0 = 0°, 20°, 40° and 60° with the help of Eq. (9) corresponding to external pressure of 0.5 GPa. The numeric values of the sesntivity of the structure with dd = 400 nm at θ0 = 0°, 20°, 40° and 60° under the influence of an external pressure 0.5 GPa are being summarized in Table 4. Form the data of the Table 4 one can easily see the effect of changing the angle of incidence from normal incidence to oblique incidence. As θ0 increases from 0°, the sesntivity of the proposed pressure sesning structure with optimized defect layer thickness dd = 400 nm increases. This increase in sesntivity is smaller under lower incident angles but significantely improves to 72 nm/GPa at θ0 = 60°. Any increase in the θ0 beyond 60° resullts the drastic fall in the intensity of defect mode with and with out external pressure. This major reduction in the intensity of the defect mode is below the threshhold value of the energy requirement of the electronic detectors used for the display the results of the sesnor.
The results of the Table 4 are plotted in Fig. 8 to observe the impact of incident angle on the sensitivity of the proposed 1d photonic pressuring sensing design with optimized defect layer thickness dd = 400 nm under the influence of an external pressure 0.5 GPa. It shows that under lower incident angles sensitivity increases nearly linear. Under higher incident angles the various of sensitivity does not follow linear relationship. Moreover, the nature of the sensitivity variations with respect to defect layer thickness and incident angles are opposite in nature as evident from Figs. 6 and 8 respectively because of their respective redshift and blueshift variations of the transmission spectra as shown in Figs. 5 and 7.

A direct relationship between the sensitivity and incident angle of the structures with dd = 400 nm under the influence of fixed external pressure of 0.5 GPa.
Finally, we have examined the performance of our 1D photonic pressure sesning structure (GaP/SiO2)N/Al2O3/(GaP/SiO2)N with optimized defect layer thickness dd = 400 nm at θ0 = 60°. This perofrmance evaluation has been done on the basis of three additional parameterts like quality factor (Qf), figure of merit (FoM) and signal-to-noise ratio (SNR) as defined in refences [X–Y]. The numeric values of Qf, FoM and SNR in addition to the sensitivity have been summarized in Table 5 below.
From the data of Table 5, one can see that the application of the external pressure on the structure displaces the central wavelength of defect mode towards higher wavelength side. The maximum displacement is corresponding to external pressure of 2.0 GPa. The sensitivity of structure reduces slightly from 72 to 66 GPa as external pressure increases from 0.5 to 2.0 GPa respectively. This variation also improves the FWHM from 0.060 to 0.225 nm. The quality factor of the proposed structure remains high as expected though it reduces as pressure increases. The figure of merit of our pressure sensor remains low and study. The signal to noise ratio values of the proposed pressure sensor increases as we apply external pressure and becomes maximum at 2.0 PGa which is another indicator showing the minute pressure sensing.
The performance of proposed pressure sensor composed of 1d DPhC has been compared with the similar kind of work carried out by various eminent photonic worker between 2012 and 2020. The comparison based on sensitivity amongst the present and past reported works has been listed in Table 6 below. This comparison helps us to infer that the proposed pressure sensor composed of (GaP/SiO2)5/Al2O3/(GaP/SiO2)5 with dd = 400 nm and θ0 = 60° shows extremely high sensitivity value of 72 nm/PGa when the externally applied pressure on the design is 0.5 (GPa). The sensitivity remains almost constant under the application of extremely high pressure of 2.0 GPa which makes our design special and useful as compared to their counterparts.
Conclusion
In conclusion, we have theoretically examined a very sensitive pressure sensor based on a 1d photonic crystal with a defect. The suggested 1d photonic structure can be used as a sensitive hydrostatic pressure sensor due to their capability of detecting a very little change in the refractive index of the acousto-optic materials used in the design under the influence of an external pressure. In this work effect of various internal and external parameters on the device performance have been studied. Our design possesses the high-quality factor value of 17,870, and maximum sensitivity of 72 nm/GPa under the externally applied pressure of 0.5 GPa. The results of this study can be utilized as a framework of constructing a top-notch pressure sensor.
Data availability
The data that support the findings of this study are available from the corresponding author upon reason-able request.
References
-
Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 58(20), 2059–2062 (1987).
Google Scholar
-
Rayleigh, L. On the maintenance of vibrations by forces of double frequency, and on the propagation of waves through a medium endowed with a periodic structure. Lond. Edinb. Dublin Philos. Mag. J. Sci. 24(147), 145–159 (1887).
Google Scholar
-
John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 58, 2486–2489 (1987).
Google Scholar
-
Ben-Ali, Y. et al. Propagation of electromagnetic waves in a one-dimensional photonic crystal containing two defects. J. Mater. Environ. Sci. 8, 870–876 (2017).
Google Scholar
-
Yang, D., Tian, H. & Ji, Y. The study of electro-optical sensor based on slotted photonic crystal waveguide. Opt. Commun. 284(20), 4986–4990 (2011).
Google Scholar
-
Fenzl, C., Hirsch, T. & Wolfbeis, O. S. Photonic crystals for chemical sensing and biosensing. Angew. Chem. Int. Ed. 53, 3318–3335 (2014).
Google Scholar
-
Shanthi, K. V. & Robinson, S. Two-dimensional photonic crystal based sensor for pressure sensing. Photonic Sens. 3(3), 248–253 (2014).
Google Scholar
-
Wu, J. & Gao, J. Low temperature sensor based on one dimensional photonic crystals with a dielectric-superconducting pair defect. Optik 126, 5368–5371 (2015).
Google Scholar
-
Sabra, W., Elsayed, H. A., Mehaney, A. & Aly, A. H. Numerical optimization of 1D superconductor photonic crystals pressure sensor for low temperatures applications. Solid State Commun. 343, 114671. https://doi.org/10.1016/j.ssc.2022.114671 (2022).
Google Scholar
-
Qutb, S. R., Aly, A. H. & Sabra, W. Salinity and temperature detection for seawater based on a 1D-defective photonic crystal material. Int. J. Mod. Phys. B 35, 2150012 (2021).
Google Scholar
-
Amiri, I. S. et al. Tri-core photonic crystal fiber based refractive index dual sensor for salinity and temperature detection. Microw. Opt. Technol. Lett. 61(3), 847–852 (2019).
Google Scholar
-
Aly, A. H., Ameen, A. A. & Vigneswaran, D. Superconductor nanometallic photonic crystals as a novel smart window for low-temperature applications. J. Supercond. Nov. Magn. 32, 91–197 (2019).
-
Arafa, A. H., Abdel Ghany, S.E.-S., Fadlallah, M. M., Salman, F. E. & Kamal, B. M. Transmission and temperature sensing characteristics of a binary and ternary photonic band gap. J. Nanoelectron. Optoelectron. 10, 9–14 (2015).
Google Scholar
-
Aly, A. H. & Sabra, W. Effective surface impedance of a high temperature superconductor. Phys. C Supercond. 495, 126–129 (2013).
Google Scholar
-
Segovia-Chaves, F. & Vinck-Posada, H. Tuning of the defect mode in a 1D superconductor-semiconductor crystal with hydrostatic pressure dependent frequency of the transverse optical phonons. Phys. C 556, 7–13 (2019).
Google Scholar
-
Zaky, Z. A. et al. Theoretical optimization of Tamm plasmon polariton structure for pressure sensing applications. Opt. Quantum Electron. 55, 738 (2023).
Google Scholar
-
Zaky, Z. A., Al-Dossari, M., Sharma, A. & Aly, A. H. Effective pressure sensor using the parity-time symmetric photonic crystal. Phys. Scr. 98(3), 035522 (2023).
Google Scholar
-
Ameen, A. A., Al-Dossari, M., Zaky, Z. A. & Aly, A. H. Studying the effect of quantum dots and parity-time symmetry on the magnification of topological edge state peak as a pressure sensor. Synth. Met. 292, 117233 (2023).
Google Scholar
-
Mehaney, A. et al. Hydrostatic pressure effects for controlling the phononic band gap properties in a perfect phononic crystal. Opt. Quantum Electron. 54, 94 (2022).
Google Scholar
-
Bouzidi, A. et al. A biosensor based on one-dimensional photonic crystal for monitoring blood glycemia. JMES 8, 3892–3896 (2017).
Google Scholar
-
Cai, Z. et al. 2D photonic crystal protein hydro gel coulometer for sensing serum albumin ligand binding. Anal. Chem. 86, 4840–4847 (2014).
Google Scholar
-
Massad-Ivanir, N. et al. Trap and track: Designing self-reporting porous Si photonic crystals for rapid bacteria detection. Analyst 139, 3885–3894 (2014).
Google Scholar
-
Shalaby, A. S. et al. Theoretical study of one-dimensional defect photonic crystal a high-performance sensor for water-borne bacteria. Opt. Quantum Electron. 53, 660. https://doi.org/10.1007/s11082-021-03291-2 (2021).
Google Scholar
-
Aly, A. H. et al. Magnetic fluid sensing and detection application of one-dimensional defective photonic structure composed of air/(SiO2/ZnSe)/D/(SiO2/ZnSe)/glass. Polym. Bull. 200, 200. https://doi.org/10.1007/s00289-023-04842-1 (2023).
Google Scholar
-
Yeh, P. Optical Waves in Layered Media (Wiley-Interscience, 2005).
-
Singh, S. P. et al. Effects of SiO2 and TiO2 fillers on thermal and dielectric properties of eco-friendly bismuth glass micro composites of plasma display panels. Bull. Mater. Sci. 33(1), 33–41 (2010).
Google Scholar
-
Upadhyaya, A. M., Srivastava, M. C. & Sharan, P. Performance analysis of optomechanical-based microcantilever sensor with various geometrical shapes. Microw. Opt. Technol. Lett. 63(4), 1319–1327 (2021).
Google Scholar
-
Awasthi, S. K., Malaviya, U. & Ojha, S. P. Enhancement of omnidirectional total-reflection wavelength range by using one-dimensional ternary photonic bandgap material. JOSA B 23, 2566–2571 (2006).
Google Scholar
-
Awasthi, S. K., Malaviya, U. & Ojha, S. P. Enhancement of omnidirectional high-reflection wavelength range in one-dimensional ternary periodic structures: A comparative study. J. Nanophotonics 2, 023505 (2008).
Google Scholar
-
Aly, A. H. et al. 1d reconfigurable bistable photonic device composed of phase change material for detection of reproductive female hormones. Phys. Scr. 96, 125533 (2021).
Google Scholar
-
Al-Dossari, M. et al. Bio-alcohol sensor based on one-dimensional photonic crystals for detection of organic materials in wastewater. Materials 15, 4012 (2022).
Google Scholar
-
Gandhi, S. & Awasthi, S. K. Analysis and detection of women’s reproductive hormones using a bistable and reconfigurable 1d annular photonic crystal composed of the Ge2Sb2Te5 phase-change material. RSC Adv. 12, 30335–30348 (2022).
Google Scholar
-
Aly, A. H. et al. Study on a one-dimensional defective photonic crystal suitable for organic compound sensing applications. RSC Adv. 11, 32973–32980 (2021).
Google Scholar
-
Aly, A. H., Mohamed, B. A., Awasthi, S. K., Abdallah, S. A. O. & Amin, A. F. MATLAB simulation-based study on poliovirus sensing through one-dimensional photonic crystal with defect. Sci. Rep. 13(1), 9422 (2023).
Google Scholar
-
Almawgani, A. H. M. et al. A theoretical approach for a new design of an ultrasensitive angular plasmonic chemical sensor using black phosphorus and aluminum oxide architecture. RSC Adv. 13(24), 16154–16164 (2023).
Google Scholar
-
Malek, C. et al. Biophotonic sensor for swift detection of malignant brain tissues by using nanocomposite YBa2Cu3O7/dielectric material as a 1D defective photonic crystal. Sci. Rep. 13(1), 8115 (2023).
Google Scholar
-
Ben-Ali, Y. et al. A high sensitivity hydrostatic pressure and temperature based on a defective 1D photonic crystal. J. Electromagn. Waves Appl. 34(15), 2030–2050 (2020).
Google Scholar
-
Olyaee, S. & Dehghani, A. A. High resolution and wide dynamic range pressure sensor based on two-dimensional photonic crystal. Photonic Sens. 2(1), 92–96 (2012).
Google Scholar
-
Tao, S., Chen, D., Wang, J., Qiao, J. & Duan, Y. A high sensitivity pressure sensor based on two-dimensional photonic crystal. Photonic Sens. 6, 137–142. https://doi.org/10.1007/s13320-016-0316-x (2016).
Google Scholar
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through large Groups Project under grant number RGP. 2/157/44.
Author information
Authors and Affiliations
Contributions
B.A.M., D.M., and A.H.A. conceived of the presented idea and developed the theory. A.H.A., B.A.M, M.A., M.S., S.K.A. and D.M. performed the computations. D.M., B.A.M. and S.K.A. wrote the manuscript with support from A. H.A. In addition, A.H.A. supervised this work. All authors discussed the results and contributed to the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and Permissions
About this article
Cite this article
Aly, A.H., Mohamed, B.A., Al-Dossari, M. et al. Ultra-sensitive pressure sensing capabilities of defective one-dimensional photonic crystal.
Sci Rep 13, 18876 (2023). https://doi.org/10.1038/s41598-023-45680-5
-
Received: 26 August 2023
-
Accepted: 23 October 2023
-
Published: 01 November 2023
-
DOI: https://doi.org/10.1038/s41598-023-45680-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.