Abstract
Testing density-dependence and path-dependence in long-term population dynamics under differentiated local contexts contributes to delineate the changing role of socioeconomic forces at the base of regional disparities. Despite a millenary settlement history, such issue has been rarely investigated in Europe, and especially in highly divided countries such as those in the Mediterranean region. Using econometric modeling to manage spatial heterogeneity, our study verifies the role of selected drivers of population growth at ten times between 1921 and 2021 in more than 8000 Italian municipalities verifying density-dependent and path-dependent dynamics. Results of global and quantile (spatial) regressions highlight a differential impact of density and (lagged) population growth on demographic dynamics along the urban cycle in Italy. Being weakly significant in the inter-war period (1921–1951), econometric models totalized a high goodness-of-fit in correspondence with compact urbanization (1951–1981). Model’s fit declined in the following decades (1981–2021) reflecting suburbanization and counter-urbanization. Density-dependence and path-dependence were found significant and, respectively, positive or negative, with compact urbanization, and much less intense with suburbanization and counter-urbanization. A spatial econometric investigation of density-dependent and path-dependent mechanisms of population dynamics provided an original explanation of metropolitan cycles, delineating the evolution of socioeconomic (local) systems along the urban-rural gradient.
Introduction
Urban cycles have been extensively studied all over the world, and especially in advanced economies, since centuries1,2,3. Being regarded as separate–and recurrent–stages of a long-term cycle, urbanisation (mostly driven by positive natural balances of population and internal migration) was found associated with settlement concentration and economic agglomeration—possibly stimulating residential mobility to outer areas as a response to congestion externalities4,5,6. The subsequent suburbanization wave has in turn affected metropolitan structures and socioeconomic functions, determining a (more or less intense) decline of central cities7,8,9. Short-haul mobility, preference for specific dwellings in rural locations and sudden changes in local job markets driven by technology and accessibility gains fueled a later counter-urbanisation10,11,12. A renewed impulse to centralised urban growth to catch the intrinsic benefits of scale economies finally characterised recent population trends in advanced countries (the so-called ’re-urbanisation’ wave).
Assuming demographic dynamics as one of the most relevant processes at the base of urban cycles, the analysis of local-scale population trends may clarify the recent evolution of cities and the emergence (or consolidation) of spatial disparities across regions and countries13,14,15,16,17,18,19,20. In Europe, a wealth of factors has reported to affect the spatial distribution of resident population21,22,23,24, including globalization, structural change of economic systems, and international migration25,26,27,28. Such trends – especially in Mediterranean Europe – have reflected intense economic downturns leading to urbanisation-reurbanisation sequences accelerated by a rapid demographic transition toward low fertility, higher life expectancy, and rising immigration6,11,29.
In this context, self-regulation of population growth is a candidate driver of demographic dynamics at regional scale30,31,32. Empirical studies have demonstrated the existence of a density-dependent regulation in human populations33,34. However, density-dependent mechanisms can explain only a part of the overall variability of demographic growth rates along urban-rural gradients35, being in turn mediated by individual choices/preferences, cultural, ethnic and religious factors, and exogenous processes of a stochastic nature. These factors were not always identifiable and easily modelled36,37,38, being associated sometimes with the notion of ‘path dependency’. Similarly to density-dependence, path-dependent regulation of population growth and decline exerted a variable impact on demographic dynamics depending on the local context, e.g. in correspondence with other socioeconomic processes that accelerate or limit its action39,40,41,42.
Temporal volatility43, spatial heterogeneity44, and the intrinsic stochasticity45 underlying the complex mosaic of growth and decline typical of human populations, all observed under demographic conditions of dynamic equilibrium46,47,48, were the characteristics of density-dependent and path-dependent mechanisms at the base of population dynamics along sufficiently long time ranges and over geographical areas large enough to be representative of short and medium-range mobility. Despite the intrinsic importance of these issues for both research and policy, empirical analyses decomposing path-dependent socioeconomic transformations from density-dependent mechanisms of population growth (and decline) were rather scarce in advanced economies42,49,50. A comparative investigation of the (positive or negative) feedback mechanisms at the base of population dynamics appears indispensable for regional science and applied economics, considering together density-dependence and path-dependence, and controlling for the role of space51,52,53 over time intervals long enough to investigate the intrinsic impact of distinctive background contexts15,50,54. In this perspective, the sequential stages of urban cycles are the appropriate background influencing density-dependent and path-dependent mechanisms of population growth and decline55. In other words, we assume that the individual stages of the cycle (namely, urbanisation, suburbanisation, counter-urbanisation, and re-urbanisation) may differently shape population dynamics, because of the diverging impact of density-dependent and path-dependent regulation along the urban-rural gradient56,57,58.
Sharing comparable demographic outcomes at the regional scale and over long time periods59, Mediterranean countries represent appropriate cases when defining internal and external factors that may influence local-scale population dynamics60,61,62. In this perspective, density-dependent and path-dependent regulation of population dynamics were tested at the municipal scale in Italy over a sufficiently long and homogeneous time interval (1921–2021) representative of sequential stages of a building cycle from urbanisation to re-urbanisation14,63,64. We adopted an econometric specification that quantifies the impact of density-dependent and path-dependent processes on population dynamics65, controlling for economic (agglomeration, scale, accessibility, amenities), and non-economic (e.g. spatial) effects42,66,67. A comparative scrutiny of models’ results will contribute regional science with a more complete understanding of metropolitan cycles – an issue of vital importance when assessing urban-rural relationships that evolve over time.
Data and methods
Study area
The investigated area includes Italy (301,330 km(^2)) geographically partitioned into three macro-regions (North, Centre, South) and 20 administrative regions68. Italy shows evident disparities in Northern and Southern Italy as far as economic growth, social development, and land resources are concerned15,69, with the latter region classified as marginal and disadvantaged70,71,72. As in other Mediterranean countries, the urban-rural divide in Italy is also particularly accentuated, delineating different socioeconomic contexts from large (and mostly mono-centric) metropolitan areas (Rome, Milan, Naples, Turin) to hyper-rural areas along the Apennine mountain chain, mainly in Southern Italy. Italy shows extensive socioeconomic disparities between Northern and Southern regions. Taken together, these features make Italy a paradigmatic case allowing a refined investigation of the interplay of environmental and socioeconomic dimensions at the base of urban cycles in Southern Europe.
Data and variables
As a basic element of European classification of territorial units, Local Administrative Units (LAU) have a key role in official statistics because of data availability from national censuses and relevance for implementation of local policy73. Since LAUs were subjected to minor changes over long observation times, Istat disseminated a homogenized list of spatial units and boundaries for cross-region and cross-country comparisons50. Estimates of resident population at this spatial level were made available at the municipal scale approximately every 10 years over a century. Homogenized census data were derived from Istat (1994) and updated from the warehouse released by the Italian National Statistical Institute. The most recent data (2021) were derived from the national population register (the base of the ‘permanent census’ progressively replacing the traditional population censuses in Italy since 2018), whose results were aligned with the 2011 (and earlier) census(es). Population size and density, as well as the annual growth rate, were the main variables in our study. Population growth rates (%) were calculated at each municipality over 10 time intervals of similar length (1921–1931, 1931–1936, 1936–1951, 1951–1961, 1961–1971, 1971–1981, 1981–1991, 1991–2001, 2001–2011, and 2011–2021). Population density (inhabitants/km2) and population size (absolute number of resident inhabitants) were calculated at the same spatial scale for 11 time points between 1921 and 2021 and expressed as logarithms63. Lagged population growth rates and population density allow an explicit test of, respectively, path-dependence and density-dependence65. Population size was used to test the importance of agglomeration, as a measure of urban concentration8.
Econometric analysis
We assumed different spatial regimes of population dynamics associated with each stage of the cycle64, modelling the variability in population growth rates ((Pop.Growth_{(t=2,1)})) as a function of (i) population growth rate ((Pop.Growth_{(t=2,1)})) in the previous (i.e. (lag_{(-1)})) time interval, (ii) population density ((Dem.Density_{(t=0)})), and (iii) the overall size of the resident population as a proxy of agglomeration ((Pop.Size_{(t=0)})), both measured at the beginning of the related observation time. The analysis has also considered (iv) an average measure of Elevation for each municipality, as derived from the official source of Istat municipal atlas, (v) a dummy of closeness to the sea coastline (Sea.Prox) classifying each municipality as ‘coastal’ (code 1) or ‘inland’ (code 0) and (vi) a dummy separating municipalities acting as the ‘head town’ (Cap.city) of a given province (with code 1) from the remaining municipalities classified with code 0. All variables were standardised prior to analysis50. Use of these variables in econometric models testing density-dependent and path-dependent mechanisms of population dynamics was discussed in42,50,63. Model specification was summarised as follows:
where (alpha) is the regression constant (model’s intercept), (beta _1, beta _2. dots , beta _6) are the regression coefficients (slope), and (epsilon) is the stochastic error of the model. Models were run controlling for time (i.e. distinguishing the impact of the four stages of the cycle mentioned above) and space (i.e. using spatial econometrics approaches whose results were compared with those from standard approaches). The adopted specification allow (i) discriminating the impact of economic from non-economic forces of population growth, (ii) distinguishing the role of density-dependent mechanisms of population growth and decline from the more general path-dependency of local population dynamics, (iii) highlighting the importance of direct spatial effects, and (iv) separating them from the indirect ones (i.e. spillovers). The individual stages of the metropolitan cycle in Italy were defined as follows63: urbanisation (1951–1981), suburbanisation (1981–2001), counter-urbanisation mixed with early re-urbanisation (2001–2021); population dynamics during inter-war decades were more mixed and prepared the system to the sudden shift toward compact urbanisation. Cross-section regressions were run assuming each observation decade as a separate stage of the cycle representative of specific socioeconomic contexts and population dynamics at the local scale. A Variance Inflation Factor (VIF) was finally calculated for each time interval. Values systematically below 5 for all variables delineate a non-redundant structure of predictors’ matrix, in line with the basic assumption of non-collinearity typical of most econometric models.
Standard models
Assuming linear changes over time in population distribution over space, Eq. (1) was preliminary tested with a linear specification adopting global Ordinary Least Squares (OLS) regressions. The models’ goodness of fit was checked by way of adjusted (R^2) coefficients and the Akaike Information Criterion (AIC). Inference on regression results (i.e. Fisher-Snedecor F tests and Student t tests respectively on the overall regression fit and on individual coefficients, testing against the null hypothesis of zero coefficients with (p < 0.001)) provided an additional criterion for model’s evaluation74. To verify the violations of the basic assumptions of a general linear model, a Durbin-Watson (DW) statistic checking for serial correlation, a Breusch-Pagan (BP) index for heteroscedasticity, and a Moran (M) spatial autocorrelation coefficient for spatial dependence of residuals were run for each model, testing for significance at (p < 0.05) against the null hypothesis of no serial correlation, no heteroscedasticity, and no spatial autocorrelation structure, respectively.
Spatially explicit models
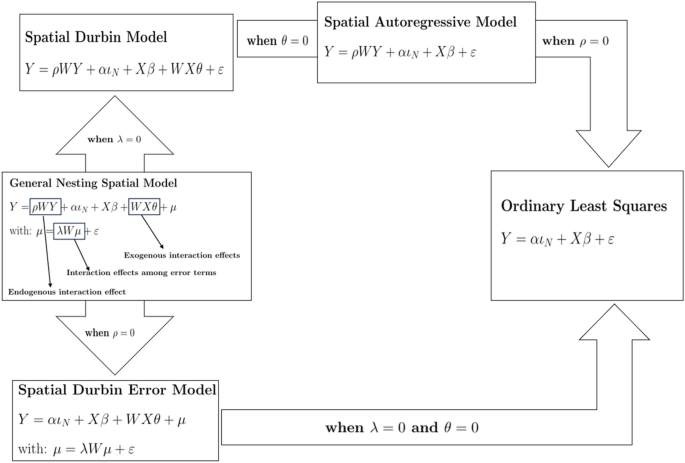
Equation (1) was additionally estimated comparing the results of global models that make spatial relations explicit using spatial weights among municipalities calculated as (i) a contiguity ((0-1)) Queen matrix (Q) and (ii) a linear distance matrix (W). While presenting a variable goodness-of-fit, consistent regression outputs (i.e. the same significant predictors with comparable intensity and sign) may identify a statistically stable (and conceptually relevant) relationship between population growth rates and the selected predictors42. By investigating the dependence of a given variable’s values on the values of the same variable recorded at neighbouring locations, spatial autocorrelation assumes outcome in one area to be affected by outcomes, covariates or errors in nearby areas, meaning that models may contain spatial lags of the outcome variable, spatial lag of covariates, and autoregressive errors, respectively56. Regressions run in this study include a Spatial Autoregressive Model (SAR), a spatial autoregressive error term (SDE), and a Spatial Durbin Model (SDM). A flowchart of the adopted spatial models has been shown in Figure 1.

Graphical description of the spatial models adopted in the work.
Both direct and indirect (spillover) effects between municipalities were detected. Best-fit estimation of the proposed models using empirical data was evaluated using pseudo (R^2). As in the case above, non-parametric (quantile) regressions with spatial weights separately from Q and W matrices were run to estimate Eq. 1 at four percentiles of the dependent variable assuming (i) deviation from normality, (ii) non-linear dependence between predictors and the dependent variable, and (iii) spatial relations among input variables. Model’s outcomes include estimates of intercept and slope coefficients and the associated significance level testing for the null-hypothesis of non-significant regression coefficient at (p < 0.05).
Results
The interwar period
Ordinary Least Square (OLS) regressions performed on standardized input variables show positive and significant values of lagged population growth rates and proximity to the sea coast despite a relatively small adjusted-(R^2) (0.05) typical of the time period (1921–1951) preceding the sharp wave of urbanisation in the aftermath of World War II. The regression coefficient for head towns is also positive. Negative and significant coefficients are observed for elevation. The variance inflation factor (VIF) is systematically low and largely below 5, suggesting a non-redundant structure of the predictor matrix (Table 1). The results obtained from quantile regressions confirm the results of the OLS regression with reference to lagged population growth, population size, elevation, proximity to the sea coast and head towns. In contrast, the differences with the OLS regression emerge when referring to population density. In general, the slope coefficients of lagged population growth rates increase from the first ((tau = 0.25)) to the fourth ((tau = 0.99)) quartile. Starting from the coefficients of the variable linked to population density, the sign–in the first three quartiles—is consistent with the one performed in the OLS, while in the fourth quartile is negative. A significant and positive coefficient is also shown by the variable linked to the size of the population from the first to the third quartile, to then become negative–even if significant–if referred to the fourth quartile. With reference to the last two variables, i.e. proximity to the sea and head town, the coefficient maintains the sign of OLS model with highly significant values in the quartiles from (tau = 0.25) to (tau = 0.75) for the first variable, and no significance in (tau = 0.99) for the first predictor. With reference to the second predictor, no coefficient appears significant except that of the third and forth quartiles, maintaining a coherent coefficient sign with OLS model. Compared to OLS models, lower AIC values have been shown in the first three quartiles of the standard quantile regression; a higher value is shown when (tau =0.99).
The results of the econometric tests indicate OLS estimations as partly biased, since tests for serial correlation, heteroscedasticity, and spatial dependence are all significant. Thus, we adopted spatial econometric techniques starting from a Spatial Durbin model (hence SDM) for the global regressions by explicitly considering the spatial structure of the input data and we compared the results with reference techniques such as Spatially Autoregressive (SAR), and Spatial Error (SDE) models. In direct and indirect SDM regressions we find positive coefficients related to the variable describing lagged population growth rates, coherently with the OLS regression. This predictor displays significant and positive coefficients for both direct and indirect effects. With reference to population size and density, elevation, as well as head town, we observe opposite signs considering direct and indirect effects. For instance, the indirect effect of population size is negative and statistically significant, while being positive but statistically insignificant when considering direct effects. Proximity to the sea coast has a positive impact (both direct and indirect) on population growth rates. Moving on to spatially quantile regressions, significant and negative coefficients were found for elevation – even if the intensity of this significance is strongest in the first three quartiles and then decreases in the fourth quartile. Positive coefficients, on average, are associated with lagged population growth and demographic density, proximity to the sea coast, and head town. Finally, the positive role of head town on population growth is positive and significant at least in the second, third and forth quartile. Positive coefficients are associated with population size in the first and second quartile, reverting to a negative coefficient in the forth quartile. Similar results were found comparing the outcomes of quantile regressions run with spatial matrices based on contiguity and linear distances among municipalities. Models based on the distance-weighted matrix tend to have lower AIC values than models based on contiguity. These results are in line with (R^2), which, in this case, shows greater values than contiguity-based spatial models. In particular, SDM performs the lowest value of AIC whereas SAR performs the greatest value of AIC in distance weighted models. When considering contiguity, SDE and SDM produce the lowest AIC values, while SAR performs the greatest AIC value. Generally speaking, the goodness of fit of spatial models is consistently higher than that of standard models.
The breakdown of intense urbanisation
Moving to the subsequent time interval, Table 2 illustrates the results of standard econometrics and spatial models using both contiguity and linear distance spatial weights. Here the results of OLS estimates and standard quantile regressions appear rather coherent in assigning positive and significant coefficients to lagged population growth rates, demographic density, proximity to the sea coast and head town, with increasing values of the adjusted-(R^2). Econometric diagnostics also indicate that the OLS estimate is (moderately) biased. The tests of serial correlation, heteroscedasticity and spatial dependence are all significant, suggesting the appropriateness of using spatial models. When comparing the econometric results from different spatial weighting schemes, models such as SAR and SDE give similar results with OLS as far as sign and significance of the regression coefficients. A general comparison of OLS values of AIC with that of spatial weighted models highlight that SAR and SDM seem to be more effective than OLS in explaining the variance of the phenomenon, while SDE has an higher value of AIC in comparison to OLS. These results are also consistent with the estimate of direct impacts from SDM. Indirect impacts from SDM are rather different from the structure of direct impacts, suggesting the role of spatial heterogeneity for specific predictors, such as demographic density, population size, and elevation. In general, regressions based on a spatially weighted distance matrix seem to perform better than those based on contiguity. With distance, the three AIC values are consistent with the corresponding (R^2) (lower in SAR and greater in SDM). With contiguity, SDM displays a lowest AIC value that corresponds to the greater (R^2) value. Considering quantile regressions, lagged population growth, elevation, and proximity to the sea coast maintain the OLS coefficients’ sign and significance almost for all quartiles. Population size coefficients were found positive for the first three quartiles, becoming negative in the fourth quartile.
Considering a subsequent time interval with intense expansion of human settlements in Italy, lagged population growth rates, demographic density, elevation, proximity to the sea coast, and head town display almost positive and significant regression coefficients both for OLS and quantile regressions, with markedly improved (R^2) (Table 3). The positive coefficients estimated for demographic density and population size are antithetical to those observed for earlier time windows. Variance inflation factors (VIFs) for each predictor are systematically less than 5, suggesting a non-redundant structure of the regressors matrix. Test diagnostics for serial correlation, heteroscedasticity, and spatial dependence suggest the appropriateness of using spatial modelling. Considering both contiguity and distance weighting, SAR and SDE results are rather consistent with those of OLS with respect to the sign of the regression coefficients. The direct effects of SDM mostly resemble the outcome of SAR and SDE models. Direct and indirect coefficients for demographic density and population size assume opposite signs. Spatial models, in general, have higher values of AIC than OLS. Quantile regressions provided similar outcomes irrespective of the spatial weighting scheme adopted.
From compact urbanisation to suburbanisation
Table 4 illustrates the results of econometric modeling investigating a distinctive time interval as far as population dynamics in Italy is concerned. Both OLS and quantile regressions improved their goodness-of-fit (adjusted-(R^2) (> 0.4)), corresponding to contained values of AIC, at least in OLS and in the first three quartiles of standard quartile regressions. Lagged population growth rates and demographic density have a positive impact of current population growth rates; population size, elevation, proximity to the sea coast and head town have a negative–while less intense and more mixed–impact on current population growth rates. Following the results of econometric diagnostics, spatial models provide outcomes adjusted to the spatial structure of both predictors and the dependent variable. However, in the essence, global spatial models give results well aligned with those of the OLS regression; moreover, spatial quantile regressions confirm the outcomes of standard quantile regressions. Coherent results are also displayed comparing adjusted-(R^2) with AIC, i.e., higher values of the first indicator correspond to lower values of the second one. Adjusted-(R^2) confirms the best performance of SDM in both cases, while low performances (low adjusted-(R^2) and high AIC), are found in the two specifications of SAR.
Results of both OLS and quantile regressions for the subsequent time interval (Table 5) are also aligned with the models’ outcomes described for the previous decade (see above), with model’s goodness-of-fit maintaining generally high. Lagged population growth rates, demographic density, and proximity to the sea coast reveal a positive and significant impact on the dependent variable. Elevation and head town show the reverse effect, while population size display more mixed results, possible associated with a higher spatial heterogeneity characteristic of this predictor. Although the non-redundant structure of predictors (VIF systematically below 2), econometric diagnostics suggested the appropriateness of spatial modelling also in this case. Improving slightly the goodness-of-fit in respect with non-spatial modeling, results of global regressions (SAR, SDE and SDM, direct effects) are mostly aligned with the OLS model. Moreover, spatial quantile regressions estimate a comparable structure of coefficients for the selected predictors, irrespective of the spatial weighting scheme. All these models show appreciable goodness-of-fit that reflects convergent results, as far as sign and significance of regression coefficients. Based on the values of AIC, the best performance is attributed to SDE and SDM weighted by distance In Table 5. Conversely, SAR model exhibits a lower value of AIC with contiguity. All outcomes are in line with adjusted-(R^2).
Moving toward counter-urbanisation
Similarly to what reported in Tables 4 and 5, modeling population growth rates between 1981 and 1991 (Table 6) with standard econometrics delineate the role of head town (negative impact) as well as lagged population growth rates and demographic density (positive impacts). In partial disagreement with what has been observed in earlier decades, population size, elevation, and proximity to the sea coast, show more heterogeneous results, with significant and non-significant coefficients and contrasting signs when moving from OLS to quantile regressions. Despite a satisfactory goodness-of-fit, econometric diagnostics suggested the use of spatial models that reached a systematically higher fit than standard models. Results of global models, irrespective of the spatial weighting scheme, confirm the role of lagged population growth rates and demographic density as predictors of current population growth rates. Outcomes from AIC, confirmed by adjusted-(R^2), follow the same tendency. Elevation and population size give more mixed, while significant, results. Quantile regressions provide useful insights when describing the latent heterogeneity associated with predictors such as population size, elevation, proximity to the sea coast and head town. For instance, the negative impact of population size is spatially polarized, i.e. higher for the forth quartile and lower moving from the third to the first quartile. A reverse pattern is observed for elevation and proximity to the sea coast.
Standard and spatial modeling explaining the variability in population growth rates (1991–2001) gain significance, with a considerable goodness-of-fit increasing further when the spatial structure of predictors is considered (Table 7). Lagged population growth rates and demographic density show a positive and highly significant coefficient irrespective of the model used. The impact of population size (negative and significant coefficients) is also homogeneous across model’s specifications. The impact of elevation is also negative, although minor differences were found comparing the results of quantile regressions run with the two spatial weighting schemes. Global models (both standard and spatial) also suggest how proximity to the sea coast exerted a negative and significant impact on the dependent variable. Quantile regressions provide similar results, with the only exception of the forth quartile. Head town as a predictor of population growth rates is associated to mostly negative coefficients (global models). Outcomes of adjusted-(R^2) and AIC, jointly confirm the better performance of distance weighted models compared to contiguity. Negative coefficients were also found in quantile regressions (both standard and spatial) for the first and the second quartiles, but not for the third and the forth quartiles.
Latent trends toward re-urbanisation
Table 8 shows the results of econometric models estimating the spatial variability of population growth rates between 2001 and 2011. All models, starting from OLS, significantly improved their goodness-of-fit compared with what has been estimated in earlier decades. Econometric diagnostics, goodness-of-fit (adjusted-(R^2) or pseudo-(R^2)) and the Akaike Information Criterion (AIC) coherently document how spatial models performed better than standard models. Concerning spatial models, in line with adjusted-(R^2), the distance weighted scenario seems to better perform than contiguity. Lagged population growth rates and demographic density have a positive and highly significant impact on the dependent variable, irrespective of the model’s specification and the spatial weighting scheme. Global and quantile models provide comparable results for these two predictors. The impact of elevation is, in turn, negative and highly significant, for all models. However, the indirect impact of this variable estimated via SDM results slightly significant or completely insignificant. The impact of the proximity to the sea coast and head town as predictors of population growth rates is negative – as depicted in the outcomes of global (both standard and spatial) econometric models – and more mixed in quantile regressions, being moderately significant for the first and second quartiles (proximity to the sea coast) and for the first and forth quartiles (head town).
The outcomes of regressions modeling the spatial variability of population growth rates between 2011 and 2021 indicate substantially different demographic dynamics, as far as intensity and spatial structure are concerned (Table 9). The overall estimate of model’s goodness-of-fit is moderate or rather low for all econometric specifications, and improved slightly moving from standard to spatial models, despite test diagnostics were convergent in suggesting the appropriateness of using spatially explicit approaches. From the results of AIC and adjusted-(R^2) in spatially weighted models, it emerges the higher fit of distance models in comparison with contiguity models. Quantile regressions performed better than global models; more specifically, results for the first and second quartiles had a satisfactory goodness-of-fit, declining for the third and forth quartiles. Among predictors, the impact of lagged population growth rates on the dependent variable is confirmed, in line with the results of estimates for previous decades, although (global) regression coefficients are less intense and significant, irrespective of the model’s specification. The same (positive) impact was found in quantile regressions (first to third quartile), with the exception of the forth quartile. The impact of demographic density is really mixed and heterogeneous moving from global to quantile regressions. Population size seems to have a slightly negative impact on the dependent variable, although econometric estimates were rather mixed, as in the case of demographic density. Elevation, proximity to the sea coast and head town display almost insignificant and close-to-zero regression coefficients, apart from few exceptions (mainly in quantile regressions).
Discussion
The present study illustrates a diachronic analysis of demographic dynamics at the municipal scale in Italy, verifying density-dependence, path-dependence, agglomeration/scale impacts, and spatial effects over a complete (demographic-urban) cycle from urbanisation to re-urbanisation. The approach developed in this study was based on the comparison of different statistical models, both parametric (global econometrics) and non-parametric (quantile regressions). This approach allowed a precise identification of the factors underlying processes of demographic growth and decline, in turn consolidating complex urban-rural hierarchies in advanced economies75. While global models provide a gross assessment of the impact of various predictors of population growth rate at a sufficiently detailed spatial scale76, quantile regressions allow an even more accurate inspection of the trends characteristic of specific parts of the statistical distribution of the dependent variable77. These statistical loci correspond to specific demographic behaviours, which reflect diversified but internally homogeneous territorial contexts. Examples include demographically dynamic contexts with positive and sustained growth rates, and demographically shrinking contexts having systematically negative growth rates. While non-spatial models (both global and quantile) provided the baseline knowledge to a refined understanding of population dynamics and the underlying factors and contexts, spatial models proved to be innovative tools analysing regional variability in the dependent variable. Moreover, the comparison between the results of global and quantile models specifying the geographical structure of the elementary units adopted in this study allows a more accurate examination of the role of spatial heterogeneity in population dynamics78. As far as the case study, while global models have satisfactorily explained population growth rates at a sufficiently detailed spatial level, the outcomes of quantile models often were in line with the results of global models. These outcomes were characteristic of the ‘urbanisation’ phase (1951–1961, 1961–1971, 1971–1981) with medium-high growth rates in Italy79. On the contrary, during the ’counter-urbanisation’ and ’re-urbanisation’ waves (1991–2001, 2001–2011, 2011–2021), global models fitted the dependent variable less effectively. At such times, quantile regressions provided likely more accurate indications of demographic behaviours in conditions of spatial heterogeneity80. This may highlight latent spatial patterns that are characteristic of territories with systematically high or low population growth rates64, in turn corresponding with specific quartiles of the statistical distribution of the dependent variable. Taken together, the results of the econometric models document how density-dependence has been observed in correspondence with urbanisation, suggesting a role for economic agglomeration and immigration24. Density-dependence was less significant over both suburbanisation and counter-urbanisation, when population tends to be more dispersed across regions44. In these contexts, the role of agglomeration and scale reduced proportionally, and path-dependent factors regulating population growth took the lead. With re-urbanisation, the positive rate of population growth observed in rural areas counterbalanced the stable (or negative) pattern observed in urban areas, indicating a relationship with population growth that reflects congestion externalities and subtle processes of peri-urbanisation intensifying in recent decades5. The outcomes of quantile regressions have more specifically delineated the existence of a non-linear relationship between population growth and density for all time intervals, although with important differences as far as the impact of individual factors is concerned. Results of quantile regressions document a positive effect of density on population growth rates, being stronger at higher levels of urban concentration, while declining slightly over time. Such findings are in line with the documented outcomes of sequential waves of urbanization, suburbanization and re-urbanization typical of post-war Italy11,49,53. In other words, the density-growth relationship is indicative of sequential stages characteristic of the metropolitan cycle in Mediterranean Europe73. All in all, our study demonstrates how sequential waves of concentration and de-concentration of urban and rural locations were associated with density-dependent mechanisms of population growth and decline. This process, shaping the expansion of rural/accessible districts, and the abandonment of marginal districts, accentuated the divide in high-density and low-density areas63,81,82. The flexibility of this approach justifies an extended use of global econometric models and quantile regressions analysing the drivers of population growth in socioeconomic contexts distinct from the one studied in this application, and at vastly differentiated (spatial and temporal) scales. An extensive use of spatial panel techniques applied to both global and quantile models is also recommended when sufficiently long time series of predictors are available at homogeneous and stable spatial units77. In addition, comparing the results of econometric models specifying multiple spatial weighting schemes (e.g. based on different contiguity and distance metrics) seems to be an appropriate tool83 when inferring about the stability of regression coefficients (sign and significance) across models84 and when taking decisions about the best performing models85. In this last case, diagnostics such as Akaike Information Criterion can easily and effectively complement such approaches86. Future studies should also investigate the appropriateness of local techniques (e.g. the Geographically Weighted Regression, GWR) to the investigation of regional variability and local heterogeneity in population dynamics87, considering both cross-section approaches and panel extensions, when input data allow such improvements. Although the process of demographic growth and decline at a local scale seem to follow similar underlying logics in various regions of Europe (for instance, in the Mediterranean countries88), a more accurate examination of the latent factors at the base of formation (and/or consolidation) of regional disparities in the geographical distribution and density of resident population may support a spatial planning aimed at a balanced, polycentric, and sustainable development of territories and local communities89. While identifying distinctive (demographic) regimes at the local scale, the empirical results of our study outline the intrinsic characteristics of local contexts and the differences in the relationship between population growth and density over time15, corroborating the assumption that density-dependent regulation was intrinsically associated with exogenous dynamics depending on urban cycles. In this perspective, long-term demographic processes in Mediterranean Europe59 can be seen as representative of more general dynamics at the continental scale. Based on a comparative approach76, our study definitely offers an exploratory econometric perspective to regional studies of population dynamics that can be easily adapted to different spatial scales (from local to regional levels), temporal schedule (from decadal to annual windows), and variables, e.g. moving from strictly demographic indicators to economic predictors of leading and lagging contexts in the old continent and beyond.
Conclusions
A spatial econometric investigation of density-dependent and path-dependent mechanisms of population dynamics provided an original explanation of metropolitan cycles, delineating the evolution of socioeconomic (local) systems along the urban-rural gradient. With accelerated population dynamics, empirical results delineate compact urbanisation (1951–1981) as the main factor consolidating spatial disparities in Italy. As a matter of fact, econometric models–being only weakly significant in the inter-war period (1921–1951) – showed a high goodness-of-fit in correspondence with compact urbanisation that declined moderately with suburbanisation and counter-urbanisation (1981–2021). Density-dependence and path-dependence were found significant and, respectively, positive and negative, with compact urbanisation, and much less intense with suburbanisation and counter-urbanisation. The results of our study justify a renewed (diachronic and spatially explicit) analysis of socioeconomic development vis à vis demographic transition processes aimed at providing a more comprehensive interpretation of metropolitan transformations and the related evolution of local contexts.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
-
Reher, D. S. The demographic transition revisited as a global process. Popul. Space Place 10, 19–41 (2004).
Google Scholar
-
Lerch, M. The role of migration in the urban transition: A demonstration from albania. Demography 51, 1527–1550 (2014).
Google Scholar
-
Salvati, L., Zambon, I., Chelli, F. M. & Serra, P. Do spatial patterns of urbanization and land consumption reflect different socioeconomic contexts in europe?. Sci. Total Environ. 625, 722–730 (2018).
Google Scholar
-
Kabisch, N. & Haase, D. Diversifying european agglomerations: Evidence of urban population trends for the 21st century. Popul. Space Place 17, 236–253 (2011).
Google Scholar
-
Gkartzios, M. ‘leaving athens’: Narratives of counterurbanisation in times of crisis. J. Rural. Stud. 32, 158–167 (2013).
Google Scholar
-
Bayona-I-Carrasco, J., Gil-Alonso, F. & Pujadas-I-Rúbies, I. Suburbanisation versus recentralisation: Changes in the effect of international migration inflows on the largest spanish metropolitan areas (2000–2010). Quetelet J. 2, 93–118 (2014).
Google Scholar
-
Henrie, C. J. & Plane, D. A. Exodus from the california core: Using demographic effectiveness and migration impact measures to examine population redistribution within the western united states. Popul. Res. Policy Rev. 27, 43–64 (2008).
Google Scholar
-
Carlucci, M., Chelli, F. M. & Salvati, L. Toward a new cycle: Short-term population dynamics, gentrification, and re-urbanization of milan (italy). Sustainability 10, 3014 (2018).
Google Scholar
-
Duvernoy, I., Zambon, I., Sateriano, A. & Salvati, L. Pictures from the other side of the fringe: Urban growth and peri-urban agriculture in a post-industrial city (toulouse, france). J. Rural. Stud. 57, 25–35 (2018).
Google Scholar
-
Allen, J., Barlow, J., Leal, J., Maloutas, T. & Padovani, L. Housing and welfare in Southern Europe, vol. 610 (Wiley Online Library, 2004).
-
Cuadrado-Ciuraneta, S., Durà-Guimerà, A. & Salvati, L. Not only tourism: Unravelling suburbanization, second-home expansion and “rural’’ sprawl in catalonia, spain. Urban Geogr. 38, 66–89 (2017).
Google Scholar
-
Rubiera-Morollon, F., ViÃuela, A. et al. Heterogeneity in the determinants of population growth at the local level. Int. Reg. Sci. Rev. 40, 211–240 (2017).
-
Alados, C. L., Errea, P., Gartzia, M., Saiz, H. & Escós, J. Positive and negative feedbacks and free-scale pattern distribution in rural-population dynamics. PLoS ONE 9, e114561 (2014).
Google Scholar
-
Gavalas, V. S., Rontos, K. & Salvati, L. Who becomes an unwed mother in greece? sociodemographic and geographical aspects of an emerging phenomenon. Popul. Space Place 20, 250–263 (2014).
Google Scholar
-
Ciommi, M., Chelli, F. M., Carlucci, M. & Salvati, L. Urban growth and demographic dynamics in southern europe: Toward a new statistical approach to regional science. Sustainability 10, 2765 (2018).
Google Scholar
-
Alaimo, L. S. & Maggino, F. Sustainable development goals indicators at territorial level: Conceptual and methodological issues-the italian perspective. Soc. Indic. Res. 147, 383–419 (2020).
Google Scholar
-
Alaimo, L. S., Ivaldi, E., Landi, S. & Maggino, F. Measuring and evaluating socio-economic inequality in small areas: An application to the urban units of the municipality of genoa. Socioecon. Plann. Sci. 83, 101170 (2022).
Google Scholar
-
Alaimo, L. S., Ciommi, M., Vardopoulos, I., Nosova, B. & Salvati, L. The medium-term impact of the covid-19 pandemic on population dynamics: The case of italy. Sustainability 14, 13995 (2022).
Google Scholar
-
Giacalone, M., Turco, R., Mosconi, E. M., Alaimo, L. S. & Salvati, L. The way toward growth: A time-series factor decomposition of socioeconomic impulses and urbanization trends in a pre-crisis european region. Soc. Indic. Res. 1–22 (2023).
-
Alaimo, L. S., Nosova, B. & Salvati, L. Did covid-19 enlarge spatial disparities in population dynamics? a comparative, multivariate approach for italy. Qual. Quant. 1–30 (2023).
-
Avdeev, A. et al. Populations and demographic trends of european countries, 1980–2010. Population 66, 9–129 (2011).
Google Scholar
-
Arapoglou, V. P. Diversity, inequality and urban change. Eur. Urban Reg. Stud. 19, 223–237 (2012).
Google Scholar
-
Brombach, K., Jessen, J., Siedentop, S. & Zakrzewski, P. Demographic patterns of reurbanisation and housing in metropolitan regions in the us and germany. Comp. Popul. Stud.-Zeitschrift für Bevölkerungswissenschaft 42, 281–317 (2017).
-
Bocquier, P. & Brée, S. A regional perspective on the economic determinants of urban transition in 19th-century france. Demogr. Res. 38, 1535–1576 (2018).
Google Scholar
-
Cheshire, P. A new phase of urban development in western europe? The evidence for the 1980s. Urban Stud. 32, 1045–1063 (1995).
Google Scholar
-
Champion, A. G. A changing demographic regime and evolving poly centric urban regions: Consequences for the size, composition and distribution of city populations. Urban stud. 38, 657–677 (2001).
Google Scholar
-
Oueslati, W., Alvanides, S. & Garrod, G. Determinants of urban sprawl in european cities. Urban Stud. 52, 1594–1614 (2015).
Google Scholar
-
Haase, A., Bernt, M., Großmann, K., Mykhnenko, V. & Rink, D. Varieties of shrinkage in European cities. Eur. Urban Reg. Stud. 23, 86–102 (2016).
Google Scholar
-
López-Gay, A. Population growth and re-urbanization in spanish inner cities: The role of internal migration and residential mobility. Revue Quetelet 1, 67–92 (2014).
Google Scholar
-
Lee, R. D. Population dynamics of humans and other animals. Demography 443–465 (1987).
-
Lutz, W., Testa, M. R. & Penn, D. J. Population density is a key factor in declining human fertility. Popul. Environ. 28, 69–81 (2006).
Google Scholar
-
Lima, M. & Berryman, A. A. Positive and negative feedbacks in human population dynamics: Future equilibrium or collapse?. Oikos 120, 1301–1310 (2011).
Google Scholar
-
Åström, M., Lundberg, P. & Lundberg, S. Population dynamics with sequential density-dependencies. Oikos 174–181 (1996).
-
Baldini, R. The importance of population growth and regulation in human life history evolution. PLoS ONE 10, e0119789 (2015).
Google Scholar
-
Cohen, J. E. Human population: The next half century. Science 302, 1172–1175 (2003).
Google Scholar
-
Getz, W. M. A hypothesis regarding the abruptness of density dependence and the growth rate of populations. Ecology 77, 2014–2026 (1996).
Google Scholar
-
Mathur, V. K., Stein, S. H. & Kumar, R. A dynamic model of regional population growth and decline. J. Reg. Sci. 28, 379–395 (1988).
Google Scholar
-
Millward, H. Evolution of population densities: Five canadian cities, 1971–20011. Urban Geogr. 29, 616–638 (2008).
Google Scholar
-
Gross, E. The role of density as a factor in metropolitan growth in the United States of America. Popul. Stud. 8, 113–120 (1954).
-
Hamilton, M. J. et al. Population stability, cooperation, and the invasibility of the human species. Proc. Natl. Acad. Sci. 106, 12255–12260 (2009).
Google Scholar
-
Turchin, P. Long-term population cycles in human societies. Ann. N. Y. Acad. Sci. 1162, 1–17 (2009).
Google Scholar
-
Benassi, F. et al. Population trends and desertification risk in a mediterranean region, 1861–2017. Land Use Policy 95, 104626 (2020).
Google Scholar
-
Nowicki, P., Bonelli, S., Barbero, F. & Balletto, E. Relative importance of density-dependent regulation and environmental stochasticity for butterfly population dynamics. Oecologia 161, 227–239 (2009).
Google Scholar
-
Ciommi, M. et al. Population dynamics and agglomeration factors: A non-linear threshold estimation of density effects. Sustainability 12, 2257 (2020).
Google Scholar
-
Fauteux, D., Stien, A., Yoccoz, N. G., Fuglei, E. & Ims, R. A. Climate variability and density-dependent population dynamics: Lessons from a simple high arctic ecosystem. Proc. Natl. Acad. Sci. 118, e2106635118 (2021).
Google Scholar
-
Reher, D. S. Economic and social implications of the demographic transition. Popul. Dev. Rev. 37, 11–33 (2011).
Google Scholar
-
Lesthaeghe, R. The second demographic transition: A concise overview of its development. Proc. Natl. Acad. Sci. 111, 18112–18115 (2014).
Google Scholar
-
Rees, P. et al. The impact of internal migration on population redistribution: An international comparison. Popul. Space Place 23, e2036 (2017).
Google Scholar
-
Zambon, I., Serra, P., Sauri, D., Carlucci, M. & Salvati, L. Beyond the ‘mediterranean city’: Socioeconomic disparities and urban sprawl in three southern european cities. Geografiska Annaler: Series B, Human Geogr. 99, 319–337 (2017).
Google Scholar
-
Salvia, R., Salvati, L. & Quaranta, G. Beyond the transition: Long-term population trends in a disadvantaged region of southern europe, 1861–2017. Sustainability 13, 6636 (2021).
Google Scholar
-
Turchin, P. Rarity of density dependence or population regulation with lags?. Nature 344, 660–663 (1990).
Google Scholar
-
Soutullo, A. et al. Density-dependent regulation of population size in colonial breeders: Allee and buffer effects in the migratory montagu’s harrier. Oecologia 149, 543–552 (2006).
Google Scholar
-
Salvati, L. & Carlucci, M. Urban growth, population, and recession: Unveiling multiple spatial patterns of demographic indicators in a mediterranean city. Popul. Space Place 23, e2079 (2017).
Google Scholar
-
Salvati, L. & Serra, P. Estimating rapidity of change in complex urban systems: A multidimensional, local-scale approach. Geogr. Anal. 48, 132–156 (2016).
Google Scholar
-
Salvati, L. & Gargiulo Morelli, V. Unveiling urban sprawl in the m editerranean region: Towards a latent u rban transformation?. Int. J. Urban Reg. Res. 38, 1935–1953 (2014).
Google Scholar
-
Partridge, M. D., Rickman, D. S., Ali, K. & Olfert, M. R. Do new economic geography agglomeration shadows underlie current population dynamics across the urban hierarchy?. Pap. Reg. Sci. 88, 445–466 (2009).
Google Scholar
-
Kroll, F. & Kabisch, N. The relation of diverging urban growth processes and demographic change along an urban-rural gradient. Popul. Space Place 18, 260–276 (2012).
Google Scholar
-
Osterhage, F. The end of reurbanisation? phases of concentration and deconcentration in migratory movements in north rhine-westphalia. Comp. Popul. Stud.-Zeitschrift für Bevölkerungswissenschaft 43, 131–156 (2018).
-
Carlucci, M., Grigoriadis, E., Rontos, K. & Salvati, L. Revisiting a hegemonic concept: Long-term ‘mediterranean urbanization’in between city re-polarization and metropolitan decline. Appl. Spat. Anal. Policy 10, 347–362 (2017).
Google Scholar
-
Leichenko, R. M. Growth and change in us cities and suburbs. Growth Chang. 32, 326–354 (2001).
Google Scholar
-
Larramona, G. Out-migration of immigrants in spain. Population 68, 213–235 (2013).
Google Scholar
-
Lande, R., Engen, S. & Sæther, B.-E. Evolution of stochastic demography with life history tradeoffs in density-dependent age-structured populations. Proc. Natl. Acad. Sci. 114, 11582–11590 (2017).
Google Scholar
-
Morelli, V. G., Rontos, K. & Salvati, L. Between suburbanisation and re-urbanisation: Revisiting the urban life cycle in a mediterranean compact city. Urban Res. Pract. 7, 74–88 (2014).
Google Scholar
-
Zambon, I., Colantoni, A. & Salvati, L. Horizontal vs vertical growth: Understanding latent patterns of urban expansion in large metropolitan regions. Sci. Total Environ. 654, 778–785 (2019).
Google Scholar
-
Salvati, L. Density-dependent population growth in southern europe (1961–2011): A non-parametric approach using smoothing splines. Reg. Stat. 10, 27–41 (2020).
Google Scholar
-
Serra, P., Vera, A., Tulla, A. F. & Salvati, L. Beyond urban-rural dichotomy: Exploring socioeconomic and land-use processes of change in spain (1991–2011). Appl. Geogr. 55, 71–81 (2014).
Google Scholar
-
Salvati, L., Ciommi, M. T., Serra, P. & Chelli, F. M. Exploring the spatial structure of housing prices under economic expansion and stagnation: The role of socio-demographic factors in metropolitan rome, italy. Land Use Policy 81, 143–152 (2019).
Google Scholar
-
Salvati, L. & Zitti, M. Assessing the impact of ecological and economic factors on land degradation vulnerability through multiway analysis. Ecol. Ind. 9, 357–363 (2009).
Google Scholar
-
Ciommi, M., Gigliarano, C., Emili, A., Taralli, S. & Chelli, F. M. A new class of composite indicators for measuring well-being at the local level: An application to the equitable and sustainable well-being (bes) of the italian provinces. Ecol. Ind. 76, 281–296 (2017).
Google Scholar
-
Lanfredi, M. et al. Early identification of land degradation hotspots in complex bio-geographic regions. Remote Sens. 7, 8154–8179 (2015).
Google Scholar
-
Delfanti, L. et al. Solar plants, environmental degradation and local socioeconomic contexts: A case study in a mediterranean country. Environ. Impact Assess. Rev. 61, 88–93 (2016).
Google Scholar
-
Quaranta, G. et al. Long-term impacts of grazing management on land degradation in a rural community of southern italy: Depopulation matters. Land Degrad. Dev. 31, 2379–2394 (2020).
Google Scholar
-
Di Feliciantonio, C. & Salvati, L. Southern’ alternatives of urban diffusion: Investigating settlement characteristics and socio-economic patterns in three m editerranean regions. Tijdschr. Econ. Soc. Geogr. 106, 453–470 (2015).
Google Scholar
-
Zambon, I., Benedetti, A., Ferrara, C. & Salvati, L. Soil matters? a multivariate analysis of socioeconomic constraints to urban expansion in mediterranean europe. Ecol. Econ. 146, 173–183 (2018).
Google Scholar
-
Ferrara, A. et al. Shaping the role of’fast’and’slow’drivers of change in forest-shrubland socio-ecological systems. J. Environ. Manage. 169, 155–166 (2016).
Google Scholar
-
LeSage, J. P. What regional scientists need to know about spatial econometrics. Rev. Reg. Stud. 44, 13–32 (2014).
-
McMillen, D. P. Quantile regression for spatial data (Springer Science & Business Media, 2012).
-
Gutiérrez-Posada, D., Rubiera-Morollon, F. & Viñuela, A. Heterogeneity in the determinants of population growth at the local level: Analysis of the spanish case with a gwr approach. Int. Reg. Sci. Rev. 40, 211–240 (2017).
Google Scholar
-
Masini, E. et al. Urban growth, land-use efficiency and local socioeconomic context: A comparative analysis of 417 metropolitan regions in europe. Environ. Manage. 63, 322–337 (2019).
Google Scholar
-
Kostov, P. & Le Gallo, J. Convergence: A story of quantiles and spillovers. Kyklos 68, 552–576 (2015).
Google Scholar
-
Duncan, S., Duncan, C. & Scott, S. Human population dynamics. Ann. Hum. Biol. 28, 599–615 (2001).
Google Scholar
-
Crescenzi, R., Luca, D. & Milio, S. The geography of the economic crisis in europe: National macroeconomic conditions, regional structural factors and short-term economic performance. Camb. J. Reg. Econ. Soc. 9, 13–32 (2016).
Google Scholar
-
Cartone, A., Postiglione, P. & Hewings, G. J. Does economic convergence hold? a spatial quantile analysis on european regions. Econ. Model. 95, 408–417 (2021).
Google Scholar
-
Billé, A. G., Benedetti, R. & Postiglione, P. A two-step approach to account for unobserved spatial heterogeneity. Spat. Econ. Anal. 12, 452–471 (2017).
Google Scholar
-
Panzera, D. & Postiglione, P. The impact of regional inequality on economic growth: A spatial econometric approach. Reg. Stud. 56, 687–702 (2022).
Google Scholar
-
Kubara, M. & Kopczewska, K. Akaike information criterion in choosing the optimal k-nearest neighbours of the spatial weight matrix. Spatial Econ. Anal. 1–19 (2023).
-
Salvati, L., Ferrara, A. & Chelli, F. Long-term growth and metropolitan spatial structures: An analysis of factors influencing urban patch size under different economic cycles. Geografisk Tidsskrift-Danish J. Geogr. 118, 56–71 (2018).
Google Scholar
-
Salvati, L., Morelli, V. G., Rontos, K. & Sabbi, A. Latent exurban development: City expansion along the rural-to-urban gradient in growing and declining regions of southern europe. Urban Geogr. 34, 376–394 (2013).
Google Scholar
-
Salvati, L. Towards a polycentric region? the socio-economic trajectory of rome, an ‘eternally mediterranean’city. Tijdschr. Econ. Soc. Geogr. 105, 268–284 (2014).
Google Scholar
Author information
Authors and Affiliations
Contributions
L.S.A. writing and formatting C.C. models and statistics F.M. models and statistics E.C. Tables and bibliographic analysis M.P. writing D.S. funding and writing revisions L.S. writing and the general idea of the work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and Permissions
About this article
Cite this article
Alaimo, L.S., Ciaschini, C., Mariani, F. et al. Unraveling population trends in Italy (1921–2021) with spatial econometrics.
Sci Rep 13, 20358 (2023). https://doi.org/10.1038/s41598-023-46906-2
-
Received: 09 May 2023
-
Accepted: 07 November 2023
-
Published: 21 November 2023
-
DOI: https://doi.org/10.1038/s41598-023-46906-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.